Hilfe zur Mengenlehre

Question

Aufgabe:

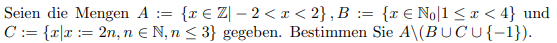
Text erkannt:

Seien die Mengen \( A:=\{x \in \mathbb{Z} \mid-2<x<2\}, B:=\left\{x \in \mathbb{N}_{0} \mid 1 \leq x<4\right\} \) und
\( C:=\{x \mid x:=2 n, n \in \mathbb{N}, n \leq 3\} \) gegeben. Bestimmen Sie \( A \backslash(B \cup C \cup\{-1\}) \)

Problem/Ansatz:

Wie ist das zu lösen? heißt ja das die Menge nur A{-1,1} sein kann oder? wie kann es dann

die Differenzmenge vo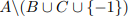n sein?

und wie würde man den Beweis bzw. das Bestimmte notieren?

Dankeschön

Text erkannt:

\( A \backslash(B \cup C \cup\{-1\}) \)

Text erkannt:

\( A:=\{x \in \mathbb{Z} \mid-2<x<2\} \)

Answer 1

heißt ja das die Menge nur A{-1,1} sein kann oder?  

nicht ganz, du hast die 0 vergessen.

"Bestimmen "  heißt doch nur:

Du sollst die Elemente der Menge angeben.