Rotationskörper Volumen A Bestimmung

Question

Text erkannt:

SChilelsen mit der x-Achse ein stück ein.
Diese Fläche rotiert um die x-Achse.
Fertigen Sie eine Skizze an und bestimmen Sie das Volumen des Rotationskörpers.
\( \Delta_{1}(a) \)
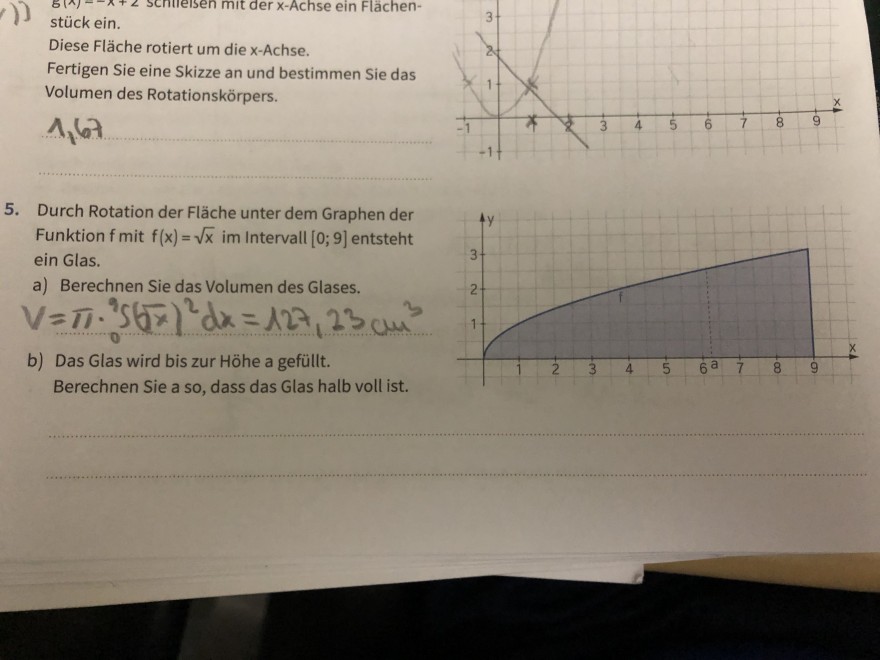
5. Durch Rotation der Fläche unter dem Graphen der Funktion \( f \) mit \( f(x)=\sqrt{x} \) im intervall \( [0 ; 9] \) entsteht ein Glas.
a) Berechnen Sie das Volumen des Glases.
b) Das Glas wird bis zur Höhe a gefüllt. Berechnen Sie a so, dass das Glas halb voll ist.

Stehe gerade auf dem Schlauch warum man bei folgender Aufgabe 5: 4,5*Wurzel 2 rechnet.

Danke

Answer 1

∫ (0 bis 9) (pi·√x^2) dx = 81/2·pi

∫ (0 bis a) (pi·√x^2) dx = 81/4·pi → a = 9/2·√2 = 6.364

Answer 2

5a) ist okay

5b)

$$a=9/\sqrt{2} ≈6,36cm→a^2=81/2$$

Comments

Warum rechnet man das so?

---

$$A=π*9^2/2$$

$$A/2=π(9/\sqrt{2})^2/2$$

Damit

$$a= 9/\sqrt{2} $$

Answer 3

π·a²/2=π·81/4   |·2/π

a²=81/2

dann ist a=9/√2≈6,364