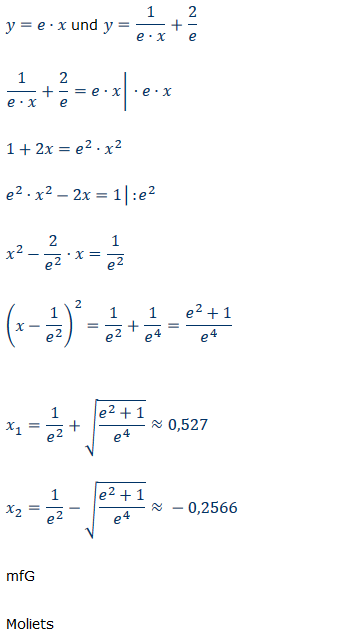
Text erkannt:
\( y=e \cdot x \) und \( y=\frac{1}{e \cdot x}+\frac{2}{e} \)
\( \frac{1}{e \cdot x}+\frac{2}{e}=e \cdot x \mid \cdot e \cdot x \)
\( 1+2 x=e^{2} \cdot x^{2} \)
\( e^{2} \cdot x^{2}-2 x=1 \mid: e^{2} \)
\( x^{2}-\frac{2}{e^{2}} \cdot x=\frac{1}{e^{2}} \)
\( \left(x-\frac{1}{e^{2}}\right)^{2}=\frac{1}{e^{2}}+\frac{1}{e^{4}}=\frac{e^{2}+1}{e^{4}} \)
\( x_{1}=\frac{1}{e^{2}}+\sqrt{\frac{e^{2}+1}{e^{4}}} \approx 0,527 \)
\( x_{2}=\frac{1}{e^{2}}-\sqrt{\frac{e^{2}+1}{e^{4}}} \approx-0,2566 \)
mfG
Moliets
Text erkannt:
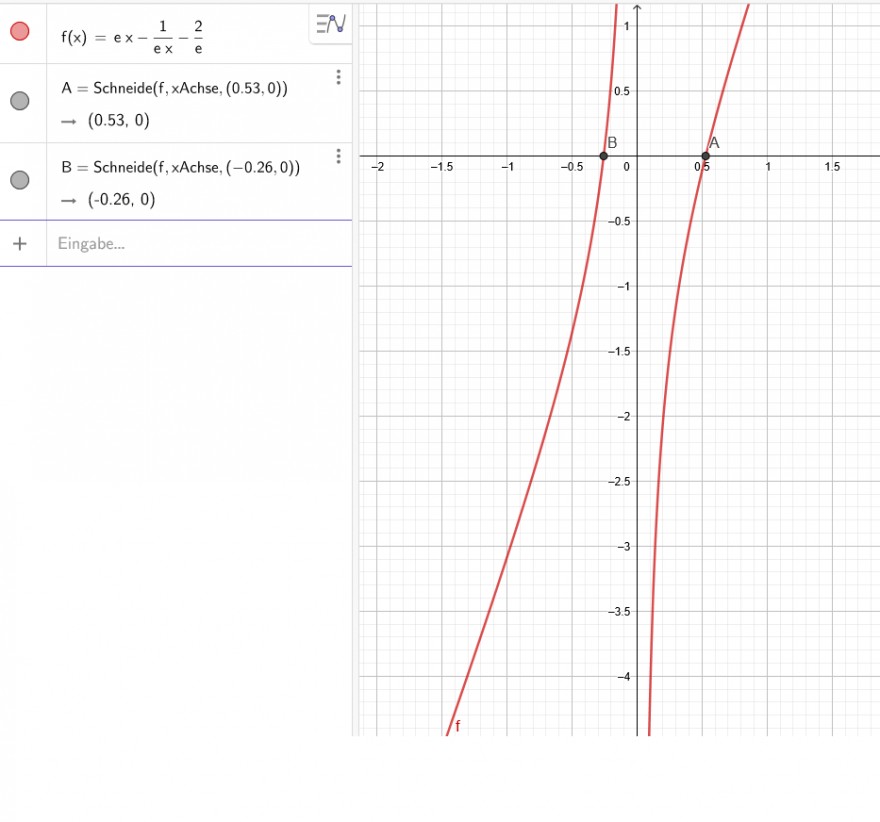
\( f(x)=e x-\frac{1}{e x}-\frac{2}{e} \)
\( \mathrm{A}= \) Schneide \( (\mathrm{f}, \mathrm{x} \) Achse \( ,(0.53,0)) \)
:
\( \rightarrow(0.53,0) \)
\( \mathrm{B}= \) Schneide \( (\mathrm{f}, \mathrm{x} \) Achse \( ,(-0.26,0)) \)
?
\( \rightarrow(-0.26,0) \)
Eingabe...