Aufgabe:
Als Geschäftsführer einer Ölfirma sei es Ihre Aufgabe, aus zehn möglichen Orten für Explorationsbohrungen die fünf Orte auszuwählen, welche die geringsten Kosten verursachen. Die Orte werden mit s1, s2, . . . , s10 und die entsprechenden Explorationskosten mit c1, c2, . . . , c10 bezeichnet. Die regionalen Verwaltungsbehörden stellen dabei folgenden Bedingungen:
(i) Bei Bohrungen bei s1 und s7 darf keine Bohrung bei s8 vorgenommen werden.
(ii) Bei Bohrung bei s3 oder s4 darf keine Bohrung bei s5 vorgenommen werden.
(iii) Aus der Gruppe der Orte s5, s6, s7, s8 Dürfen höchstens zwei ausgewählt werden.
Formulieren Sie ein lineares ganzzahliges Optimierungsproblem, um die fünf Orte für Bohrungen zu bestimmen, welche die obigen Bedingungen zu minimalen Kosten erfüllen.
Problem/Ansatz:
Wie kann man (i) darstellen? 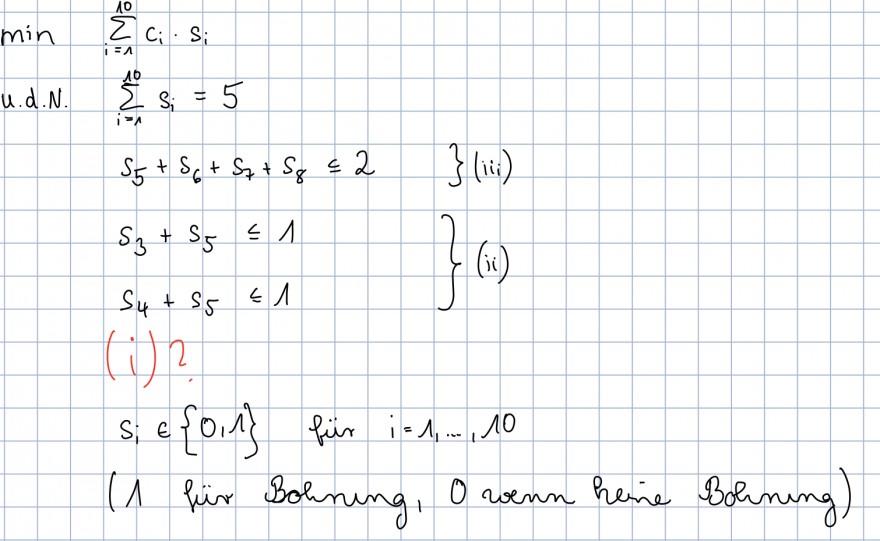
Text erkannt:
\( \min \sum \limits_{i=1}^{10} c_{i} \cdot s_{i} \)
u.d.N. \( \quad \sum \limits_{i=1}^{10} s_{i}=5 \)
\( \left.s_{5}+s_{6}+s_{7}+s_{8} \leq 2 \quad\right\}(i i) \)
\( \left.\begin{array}{l}s_{3}+s_{5} \leq 1 \\ s_{4}+s_{5} \leq 1\end{array}\right\} \)
\( (i)^{2} \)
\( s_{i} \in\{0,1\} \quad \) fin \( i=1, \ldots, 10 \)