Hab mal ein Beispiel gerechnet. Für die erste Dgl. ergibt sich folgender Lösungsverlauf \( \ddot s +\frac{1}{2}\dot s + 20s = 0 \)
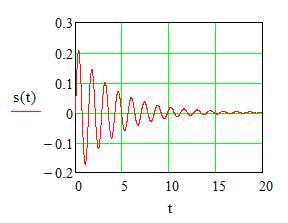
Und für die zweite folgendes \( \ddot s +\frac{1}{2}\dot s + \frac{1}{20}s = 0 \)
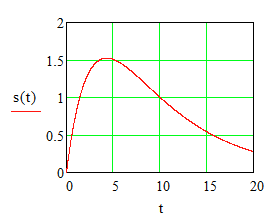
Also einmal eine gedämpfte Schwingung und einmal eine aperiodische Bewegung.
Anfangsbedingung war jedesmaö \( s(0) = 0 \) und \( \dot s(0) = 1 \)