Hallo Maria,
Willkommen in der Mathelounge!
Ich weiß, dass mann das Kommutativgesetz anwenden muss. Nur wie?
Du sollst es nicht anwenden, sondern beweisen, dass das Kommutativgesetz bei der Gleitspiegelung gilt. Sei \(V\) die Verschiebung und \(S\) die Spiegelung, so ist zu zeigen, dass $$S \circ V = V \circ S$$das kann man u.a. geometrisch oder analytisch zeigen. Geometrisch ist es anschaulich:
Ein Punkt \(P\) soll an einer Geraden \(g\) (lila) gespiegelt werden und um \(v\) (roter Pfeil) verschoben werden. Mit der Spiegelung kommt man zu \(P_S\) und mit der Verschiebung zu \(P_T\)$$P_S = S(P), \quad P_T=V(P)$$gilt das Kommutativgesetz, so muss gelten$$P' = V(S(P)) = S(V(P))$$
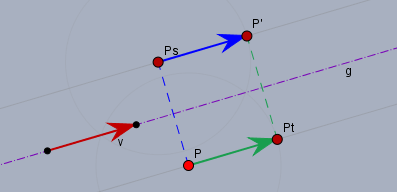
Oben im Bild siehst Du, dass die Punkte \(P\), \(P_T\), \(P'\) und \(P_S\) ein Rechteck bilden, da die Spiegelung immer senkrecht auf der Verschiebung steht. Und bei einem Rechteck ist es egal, welchen Weg man von einer Ecke (hier \(P\)) zur gegenüberliegenden Ecke (hier \(P'\)) nimmt.
Analytisch ist es etwas aufwendiger: Eine Spiegelung an einer Geraden \(g\) mit $$g: \space \vec n \vec x = d$$lässt sich (in homogenen Koordinaten) beschreiben als$$\vec p_s = S \cdot P = \left( \begin{array}{c|c} \underline 1 - \frac {2 \vec{n} \vec{n}^T}{|\vec{n}|^2} & \frac {2 d \vec n}{|\vec{n}|^2} \\ \underline 0^T& 1\end{array}\right) \begin{pmatrix} \vec p\\1 \end{pmatrix}$$und eine Verschiebung mit $$\vec{p}_t = T \cdot P = \left( \begin{array}{c|c} \underline 1& \vec v\\ \underline 0^T& 1\end{array}\right) \begin{pmatrix} \vec p\\1 \end{pmatrix} \quad \vec v \perp \vec n$$Das liest sich vielleicht kompliziert, letzteres ist aber schlicht \(\vec p_T= \vec p + \vec v\), wenn man es ausmultipliziert. Die Matrixschreibweise habe ich gewählt, da ich \(S\) und \(T\) nun multiplizieren kann. Es ist $$\begin{aligned} S \circ V &\to S \cdot V \\&= \left( \begin{array}{c|c} \underline 1 - \frac {2 \vec{n} \vec{n}^T}{|\vec{n}|^2} & \frac {2 d \vec n}{|\vec{n}|^2} \\ \underline 0^T& 1\end{array}\right) \cdot \left( \begin{array}{c|c} \underline 1& \vec v\\ \underline 0^T& 1\end{array}\right) \\&= \left( \begin{array}{c|c} \underline 1 - \frac {2 \vec{n} \vec{n}^T}{|\vec{n}|^2} & \left( \underline 1 - \frac {2 \vec{n} \vec{n}^T}{|\vec{n}|^2} \right) \vec v+ \frac {2 d \vec n}{|\vec{n}|^2} \\ \underline 0^T& 1\end{array}\right) \\&= \left( \begin{array}{c|c} \underline 1 - \frac {2 \vec{n} \vec{n}^T}{|\vec{n}|^2} & \vec v+ \frac {2 d \vec n}{|\vec{n}|^2} \\ \underline 0^T& 1\end{array}\right) \end{aligned}$$Da \(\vec n\) und \(\vec v\) senkrecht zueinander stehen, ist \(\vec n^T \vec v = 0\); folglich vereinfacht sich der Term in der beschriebenen Weise. Und umgekehrt ist $$\begin{aligned} V \circ S &\to V \cdot S \\&= \left( \begin{array}{c|c} \underline 1& \vec v\\ \underline 0^T& 1\end{array}\right) \cdot \left( \begin{array}{c|c} \underline 1 - \frac {2 \vec{n} \vec{n}^T}{|\vec{n}|^2} & \frac {2 d \vec n}{|\vec{n}|^2} \\ \underline 0^T& 1\end{array}\right) \\&= \left( \begin{array}{c|c} \underline 1 - \frac {2 \vec{n} \vec{n}^T}{|\vec{n}|^2} & \frac {2 d \vec n}{|\vec{n}|^2} + \vec v \\ \underline 0^T& 1\end{array}\right) \end{aligned}$$Ist also das gleiche. q.e.d.