berechne den Inhalt der Fläche, die der Graph der Funktion f mit der 1.

Question

Aufgabe:

berechne den Inhalt der Fläche, die der Graph der Funktion f mit der 1. Achse einschließt

Problem/Ansatz:

a) -x^2+3x -> 4,5FE

b)x^3-5x^2+6x -> 2,25FE

c) x^4-5x^2+4 -> weiß ich nicht

Answer 1

Hallo,

Denke, das die 1. Achse , die x-Achse ist

a) ist richtig

b) ich habe 37/12 (≈ 3.083) erhalten

c)  x^4-5x^2+4 =0 ->z=x^2

z^2 -5z+4=0

z_1,2= 5/2 ± √ (25/4 -16/4)

z_1,2= 5/2 ± 3/2

z₁= 4

z₂= 1

Resubstitution:

x^2=4 ------>x1.2=± 2

x^2=1------->x3.4= ±1

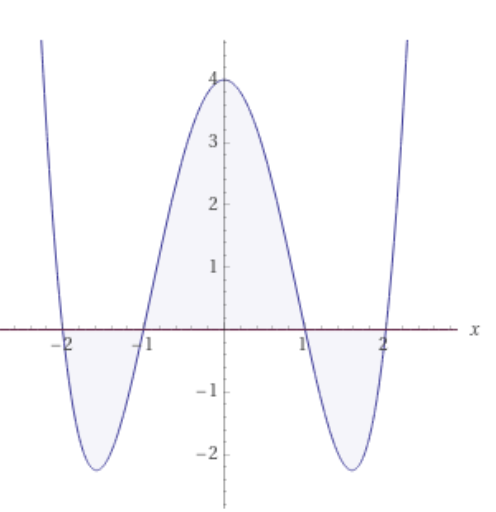
Ich habe 8 als Lösung erhalten

Comments

Haben sie für b einen Rechenweg, damit ich nachvollziehen kann was ich falsch gemacht habe?

---

∫ (x^3 -5x^2 +6)dx von 0 bis 2 +|∫ (x^3 -5x^2 +6)dx| von 2 bis 3

∫ (x^3 -5x^2 +6)dx =x^4/4  -(5/3) x^3 +6x +C , dann jeweils die Grenzen einsetzen

 =8/3 + |-5/12) =37/12

Answer 2

Bei b) hast du die Fläche die unterhalb der Abszisse liegt, mit einem Inhalt von \( \frac{5}{12} \) , abgezogen.

Bei c) ist der Flächeninhalt \( \frac{22}{15} \) von -2 bis -1, \( \frac{76}{15} \) von -1 bis 1 und wieder \( \frac{22}{15} \) von 1 bis 2.