hallo,
eine Linearkombination zweier Vektoren \(u\) und \(v\) ist ein Ausdruck wie \(r\cdot u + s \cdot v\) wobei \(r\) und \(s\) 'normale' Zahlen sind. Im Falle des Vektors $$A = \begin{pmatrix}5\\ 5\\ 4\end{pmatrix}$$ kann \(A\) auch als $$A = 2u + \frac 14 v = 2 \begin{pmatrix}1\\ 2\\ 1\end{pmatrix} + \frac 14 \begin{pmatrix}12\\ 4\\ 8\end{pmatrix} = \begin{pmatrix}5\\ 5\\ 4\end{pmatrix}$$geschrieben werden. Bei dem Vektor \(B=\begin{pmatrix}5& 4& 4\end{pmatrix}^T\) ist das nicht möglich. Es gibt keine zwei Zahlen \(r\) und \(s\), die die Gleichung $$\begin{pmatrix}5\\ 4\\ 4\end{pmatrix} = r\begin{pmatrix}1\\ 2\\ 1\end{pmatrix} + s\begin{pmatrix}12\\ 4\\ 8\end{pmatrix}$$erfüllen. Du kannst es ja mal mit \(r=7/5\) und \(s=43/140\) versuchen. Man kommt nah an \(B\) heran, aber man erreicht \(B\) nicht.
Bildlich kann man sich das so vorstellen:
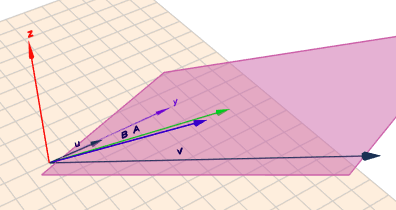
\(u\) und \(v\) (schwarz) spannen eine Ebene auf. Liegt ein dritter Vektor (z.B. A (grün)) in der Ebene, kann man mit einer Kombination der beiden Vektoren \(u\) und \(v\) den Vektor \(A\) erreichen. Liegt er nicht in dieser Ebene, so wie \(B\) (blau), dann eben nicht. Um zu sehen, dass \(B\) nicht in der Ebene liegt, muss man die Szene etwas rotieren:
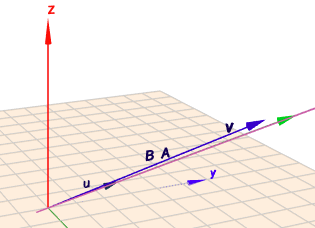
(klick auf eines der Bilder)
Um das rechnerisch zu prüfen, kann man die Gleichung für zwei der drei Koordinaten lösen - also z.B. bei \(A\)$$ r + 12s = 5 \\ 2r + 4 s = 5$$das Ergebnis wäre \(r=2\) und \(s=0,25\), und setzt das für die dritte Kordinate ein. Geht die letzte Gleichung auf, $$r + 8 s = 1 \cdot 2 + 8 \cdot \frac 14 = 4 \space \checkmark$$ist die Linearkombination möglich, falls nicht, ist sie nicht möglich.