\( G_{1}:=\left\{x \in \mathbb{R}^{3} \mid \exists s \in \mathbb{R}: x=\left(\begin{array}{l}1 \\ 2 \\ 0\end{array}\right)+s\left(\begin{array}{l}2 \\ 1 \\ 2\end{array}\right)\right\} \)
\( G_{2}:=\left\{x \in \mathbb{R}^{3} \mid \exists t \in \mathbb{R}: x=\left(\begin{array}{c}-5 \\ 13 \\ 16\end{array}\right)+t\left(\begin{array}{l}1 \\ 0 \\ 4\end{array}\right)\right\} \)
Aufgabe: Ermitteln Sie die Richtung ihres gemeinsamen Normalenvektors.
Text erkannt:
4
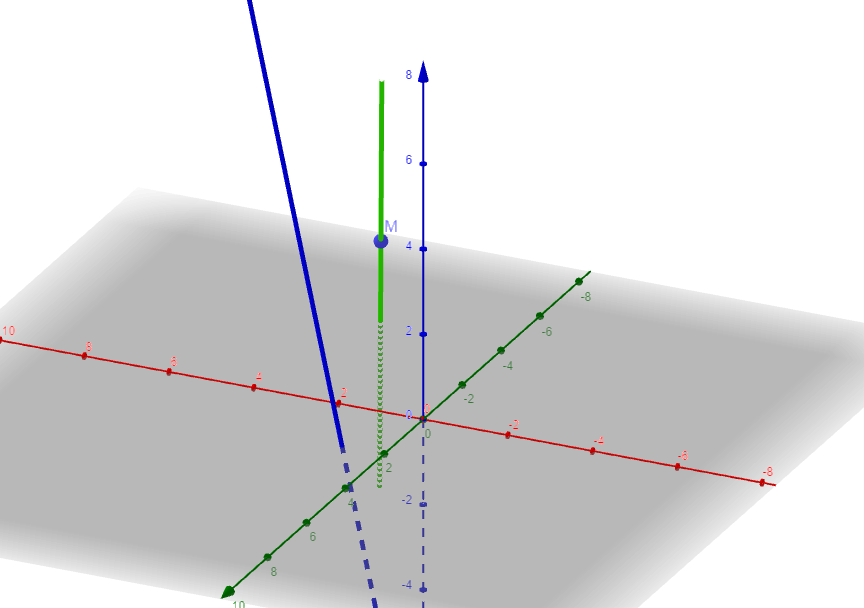
Ich habe die hier mal gezeichnet. Ich soll ja den Vektor bestimmen, der beiden berührt und das im Winkel von 90 Crad.
Aber die stehen nicht so gegenüber, dann die sich im 90 Crad Winkel schneiden könnten.
Wie kann ich das machen?