Berechnen Sie, für welche Seitenlänge man das Rechteck mit dem größten Flächeninhalt erhält.

Question

Aufgabe:

Gegeben ist die Funktion f mit f(x) = 1/25 x⁴ -2/3 x² +9/5

deren Graph mit der x-Achse im 1. Quadranten und 2. Quadranten eine Fläche einschließt. Diese Fläche soll ein achsenparalleles Rechteck einbeschrieben werden.

a) Berechnen Sie, für welche Seitenlänge man das Rechteck mit dem größten Flächeninhalt erhält.

b) Wie groß ist der maximale Flächeninhalt und wie lang sind dann die Rechteckseiten?

Answer 1

Zuerst einmal würde ich mir klar machen, wie die Funktion aussieht:

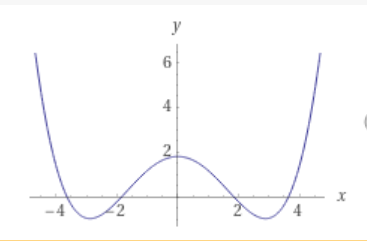
Dann sieht man, dass das Rechteck maximalen Flächeninhalt hat, wenn seine rechte Hälfte maximalen Flächeninhalt hat.

Die Formel dafür ist Breite mal Höhe = x * f(x) und die ist maximal bei x=1 weil deren erste Ableitung dort eine Nullstelle hat. Die Breite des maximalen Rechtecks ist also 2 (nämlich von -1 bis 1), seine Höhe f(1).