Erweitere mit dem Zähler. Dann steht im Nenner die 3. binomische Formel und im Zähler die erste.
Dadurch fällt im Nenner die Wurzel weg.
:-)
Wolframalpha liefert als Vereinfachung:
\( \left\{\begin{array}{l}\dfrac{2}{x}\quad\text{falls }-2 <x<2 \\[4mm] \dfrac{x}{2} \quad\text{falls } |x|>2\end{array}\right. \)
Ich merke gerade, dass das nicht stimmen kann, da der Term für -2≤x≤+2 gar nicht definiert ist. (Vermutlich geht Wolfram von komplexen Zahlen aus.)
Richtig ist für reelle x-Werte
\( \dfrac{x}{2} \quad\text{falls } |x|>2\)
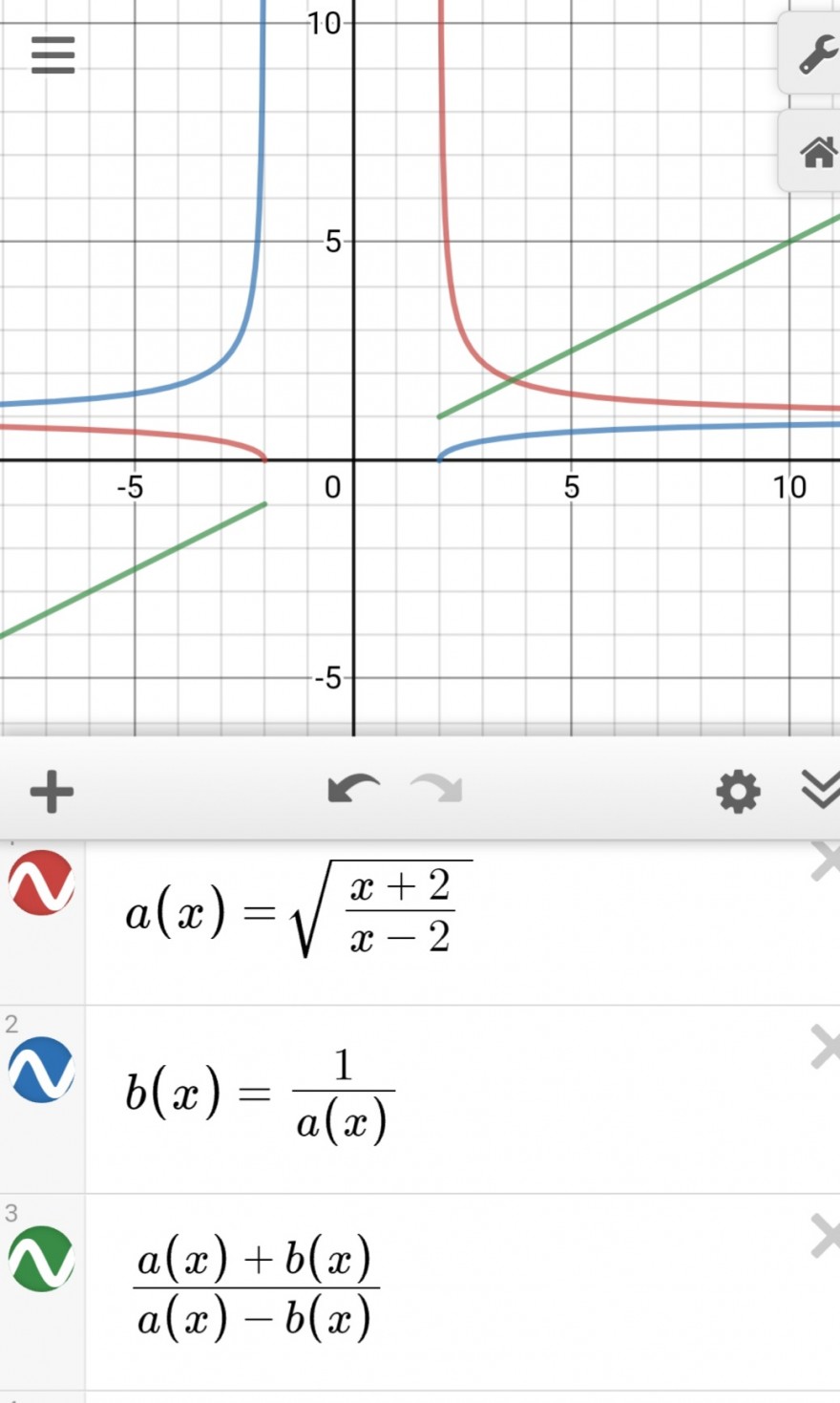
Nun noch der Graph.
Die grüne unterbrochene Gerade ist der gesuchte Graph.