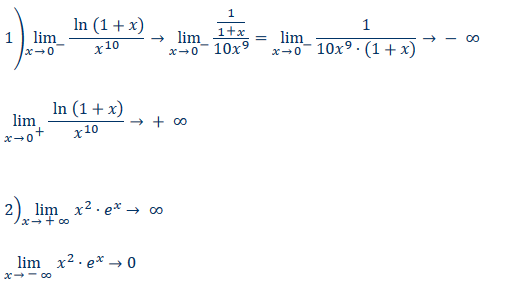
Text erkannt:
\( A \)
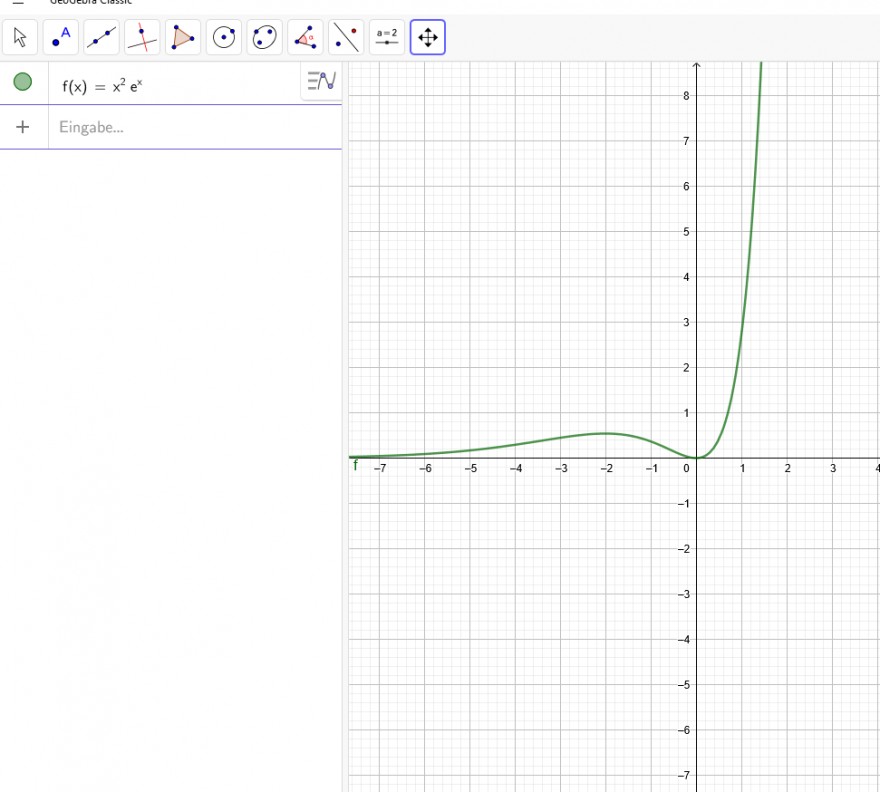
\( f(x)=\frac{\ln (1+x)}{x^{10}} \)
Text erkannt:
\( +\quad \) Eingabe...
Text erkannt:
1) \( \lim \limits_{x \rightarrow 0^{-}} \frac{\ln (1+x)}{x^{10}} \rightarrow \lim \limits_{x \rightarrow 0^{-}} \frac{\frac{1}{1+x}}{10 x^{9}}=\lim \limits_{x \rightarrow 0}-\frac{1}{10 x^{9} \cdot(1+x)} \rightarrow-\infty \)
\( \lim \limits_{x \rightarrow 0^{+}} \frac{\ln (1+x)}{x^{10}} \rightarrow+\infty \)
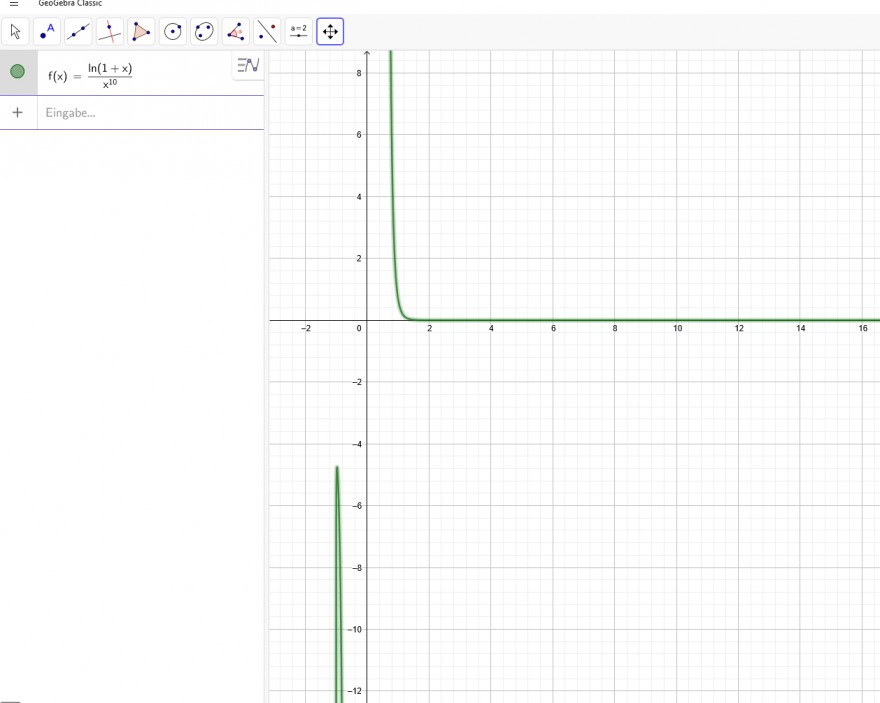
2) \( \lim \limits_{x \rightarrow+\infty} x^{2} \cdot e^{x} \rightarrow \infty \)
\( \lim \limits_{x \rightarrow-\infty} x^{2} \cdot e^{x} \rightarrow 0 \)
mfG
Moliets