Aufgabe: bestimmen Sie nun den Grenzwert der Zahlenfolge
dn+1= 1/4+d2n mit 0≤d0≤1/2
Begründen Sie, dass die Folge dn divergiert für den Startwert d0 > 1/2
Problem/Ansatz: Mein Ansatz
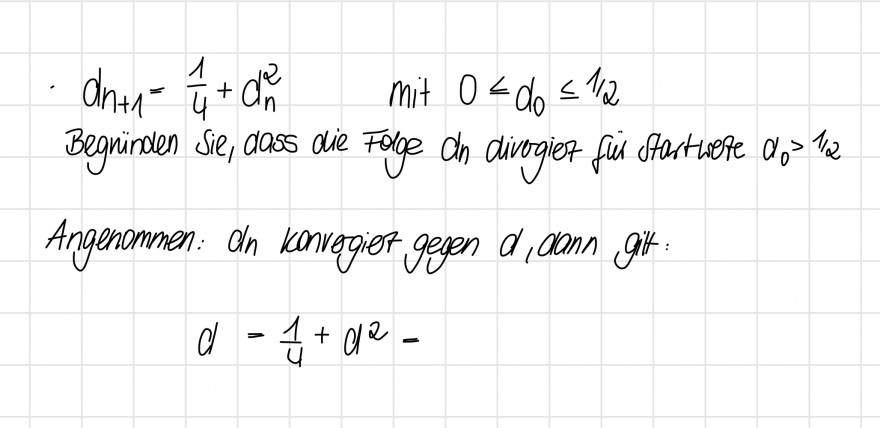
Text erkannt:
\( d_{n+1}=\frac{1}{4}+a_{n}^{2} \quad \) mit \( 0 \leq \alpha_{0} \leq 1 / 2 \)
Begninden sie, dass die Folge an divogiet fui startivere \( a_{0}>1 / 2 \)
$$ d=\frac{1}{4}+d^{2}- $$