Aufgabe:
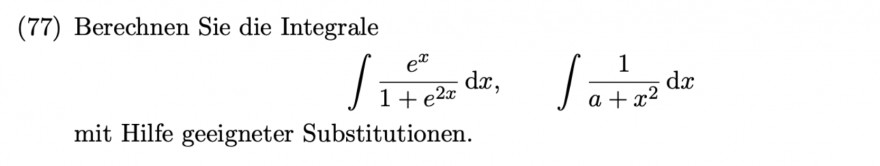
Text erkannt:
(77) Berechnen Sie die Integrale
$$ \int \frac{e^{x}}{1+e^{2 x}} \mathrm{~d} x, \quad \int \frac{1}{a+x^{2}} \mathrm{~d} x $$
mit Hilfe geeigneter Substitutionen.
zu dem zweiten Integral: mir war nicht klar was ich substituieren sollte also habe ich es in den Integralrechner eingegeben aber ich kann weder die Substitution noch den folgenden Rechenweg nachvollziehe. Ich bitte um eine Erklärung, vielen Dank!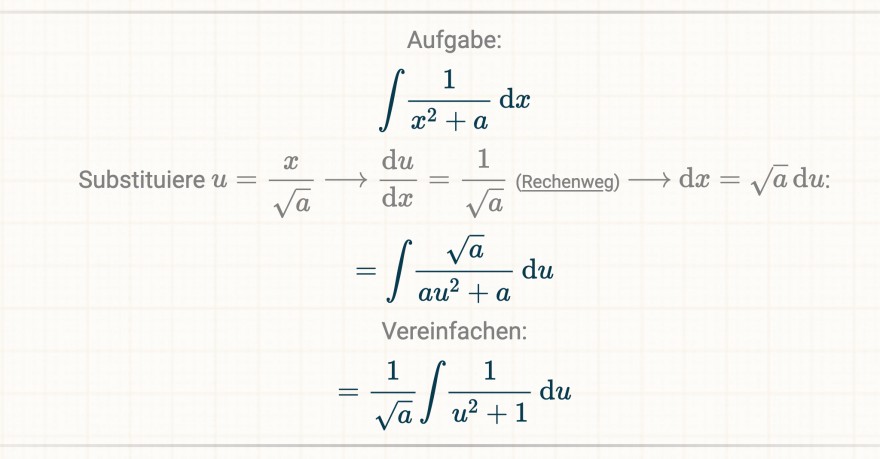
Text erkannt:
Aufgabe:
$$ \begin{array}{c}\int \frac{1}{x^{2}+a} \mathrm{~d} x \\ \text { Substituiere } u=\frac{x}{\sqrt{a}} \longrightarrow \frac{\mathrm{d} u}{\mathrm{~d} x}=\frac{1}{\sqrt{a}}(\text { Rechenweg }) \longrightarrow \mathrm{d} x=\sqrt{a} \mathrm{~d} u: \\ =\int \frac{\sqrt{a}}{a u^{2}+a} \mathrm{~d} u\end{array} $$
Vereinfachen:
\( =\frac{1}{\sqrt{a}} \int \frac{1}{u^{2}+1} \mathrm{~d} u \)