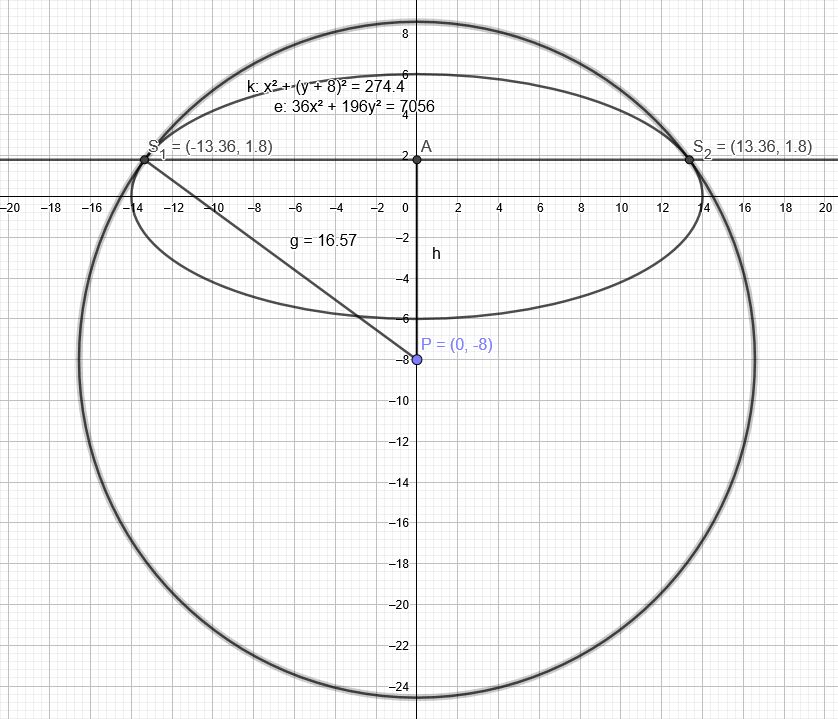
Weg über das implizite Differenzieren:
\(e(x,y)=36x^2+196y^2-7056\) vom Punkt P\( (0|−8)\)
\(e_x(x,y)=72x\)
\(e_y(x,y)=392y\)
\(e'(x)=-\frac{e_x(x,y)}{e_y(x,y)}=-\frac{9x}{49y}\)
Kreis um P\( (0|−8)\):
\(k(x,y)=x^2+(y+8)^2-r^2\)
\(k_x(x,y)=2x\)
\(k_y(x,y)=2(y+8)\)
\(k'(x)=-\frac{x}{y+8}\)
Im Schnittpunkt müssen die Tangentensteigungen gleich sein:
\(-\frac{9x}{49y}=-\frac{x}{y+8}\)
\(y=\frac{9}{5}\) einsetzen in e \(36x^2+196y^2=7056\):
\(36x^2+196\cdot \frac{81}{25}=7056\)
\(x_1=\frac{7}{5}\sqrt{91}\)
\(x_2=-\frac{7}{5}\sqrt{91}\)
Maximaler Abstand:
k: \((\frac{7}{5}\sqrt{91})^2+(1,8+8)^2=r^2\)
\(274,4=r^2\)
\(r=16,565\)