Wie hoch ist das Fenster und wie hoch ist die Unterkante über den Platz?

Question

Aufgabe:

Auf einem waagerechten Platz steht ein Gebäude mit einem Fenster ein Beobachter, dessen Augen Höhe 1,70 m beträgt und der 30 m von dem Gebäude entfernt ist sieht die Unterkante des Fensters unter dem Höhenwinkel Alpha ist gleich 21,8° und dessen Oberkante unter dem Höhenwinkel Beta ist gleich 24,2°. Wie hoch ist das Fenster und wie hoch ist die Unterkante über den Platz?

Problem/Ansatz:

Kann mir jemand erklären wie man das berechnet ich weiß nicht ganz wie ich anfangen soll vielen lieben Dank mit Rechengang und Erklärung bitte danke!

Answer 1

Hallo,

ich weiß nicht ganz wie ich anfangen soll

Beginne immer mit einer Skizze!

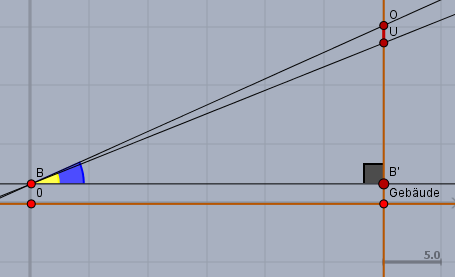
Der Punkt \(B\) steht für die Augen des Beobachters. Das Fenster im Gebäude geht von Unterkante \(U\) bis Oberkante \(O\). Die Dreiecke \(\triangle BB'U\) und \(\triangle BB'O\) sind rechtwinklig. Man geht davon aus, dass die Wand des Gebäudes senkrecht steht. Der gelbe Winkel ist \(\alpha = 21,8°\) und der blaue \(\beta = 24,2°\).

Im rechtwinkligen Dreieck gilt:$$\tan(\alpha ) = \frac{\text{Gegenkathete}}{\text{Ankathete}} = \frac{|B'U|}{|BB'|} \\ \implies |B'U| = |BB'| \cdot \tan(\alpha) = 30\,\text{m} \cdot \tan(21,8°) \approx 12,00\,\text{m}$$und weiter ist$$\tan(\beta) = \frac{|B'O|}{|BB'|} \\ \implies |B'O| = |BB'| \cdot \tan(\beta) = 30,\text{m} \cdot \tan(24,2°) \approx 13,48\,\text{m}$$Somit ist die Höhe des Fensters$$|UO| = |B'O| - |B'U| \approx 1,48\,\text m$$und die Höhe der Unterkante über dem Platz ist$$|GU| = |GB'| + |B'U| = 1,7\,\text m + 12\, \text m = 13,7\, \text m$$