Zunächst sollte man die Definitionslücken finden, falls vorhanden.
Bei Brüchen darf der Nenner nicht den Wert Null annehmen. Daher liegen bei Brüchen in der Regel Definitionslücken dort vor, wo die Nenner den Wert Null annehmen. Das ist bei den vorliegenden Brüchen bei x = - 1 bzw. x = 1 der Fall, denn bei x = - 1 nimmt der erste Bruch und bei x = 1 der zweite Bruch den Wert Null an. Die Definitionmenge ist also:
D = R \ { - 1; 1 }
Zur weiteren Lösung ist es im Folgenden erforderlich mit den Nennern der Brüche zu multiplizieren. Da diese aber an den Definitionslücken ihr Vorzeichen wechseln, muss man dabei auf die Richtung des Ungleichheitszeichens achten, denn multipliziert man mit einem negativen Wert, dann muss man das Ungleichheitszeichen umkehren.
Deshalb muss man die Ungleichung in verschiedenen Intervallen untersuchen (Fallunterscheidung), nämlich in dem Intervall, links von der ersten Definitionslücke, dann in dem/den Intervall(en) zwischen den einzelnen Definitionslücken und schließlich in dem Intervall rechts von der letzten Definitionslücke.
Vorliegend hat man zwei Definitionslücken, man muss also drei Fälle unterscheiden:
Fall 1: x < - 1
Fall 2: - 1 < x < 1
Fall 3: x > 1
Fall 1: x < - 1
Dann ist in 1 / ( x + 1 ) ≥ 2 / ( x 2 - 1) der erste Nenner negativ, während der zweite positiv ist. Also:
1 / ( x + 1 ) ≥ 2 / ( x 2 - 1)
[Multiplikation mit den Nennern, einer davon ist negativ, also Umkehrung des Ungleichheitszeichens:]
<=> x 2 - 1 ≤ 2 ( x + 1 ) = 2 x + 2
<=> x 2 - 2 x ≤ 3
<=> x 2 - 2 x + 1 ≤ 4
<=> ( x - 1 ) 2 ≤ 4
<=> | x - 1 | ≤ 2
<=> - 2 ≤ x - 1 ≤ 2
<=> - 1 ≤ x ≤ 3
Da in diesem Fall x < - 1 vorausgesetzt wurde, ist die Ungleichung in diesem Fall für kein x wahr.
Fall 2: - 1 < x < 1
Dann ist in 1 / ( x + 1 ) ≥ 2 / ( x 2 - 1) der erste Nenner positiv, während der zweite negativ ist, also:
1 / ( x + 1 ) ≥ 2 / ( x 2 - 1)
[Multiplikation mit den Nennern, einer davon ist negativ, also Umkehrung des Ungleichheitszeichens:]
<=> ...
man erhält das gleiche Ergebnis wie in Fall 1, also:
<=> - 1 ≤ x ≤ 3
allerdings unter der Voraussetzung -1 < x < 1 , sodass die Ungleichung in diesem Falle wahr ist in dem Intervall:
-1 < x < 1
Fall 3: x > 1
Dann sind in 1 / ( x + 1 ) ≥ 2 / ( x 2 - 1) beide Nenner positiv, also:
1 / ( x + 1 ) ≥ 2 / ( x 2 - 1)
[Multiplikation mit den Nennern, beide sind positiv, also keine Umkehrung des Ungleichheitszeichens:]
<=> x 2 - 1 ≥ 2 ( x + 1 ) = 2 x + 2
<=> x 2 - 2 x ≥ 3
<=> x 2 - 2 x + 1 ≥ 4
<=> ( x - 1 ) 2 ≥ 4
<=> | x - 1 | ≥ 2
<=> x - 1 ≤ - 2 oder x - 1 ≥ 2
<=> x ≤ - 1 oder x ≥ 3
Da in diesem Fall x > 1 vorausgesetzt wurde, ist die Ungleichung in diesem Fall wahr in dem Intervall:
x ≥ 3
Fasst man die drei Fälle zusammen erhält man:
1 / ( x + 1 ) ≥ 2 / ( x 2 - 1)
<=> -1 < x < 1 oder x ≥ 3
Hier ein Schaubild der Situation:
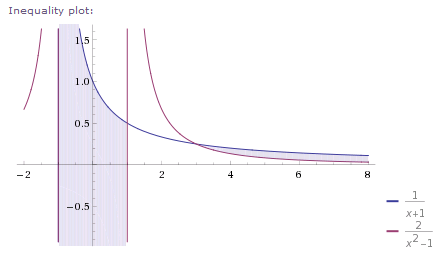
https://www.wolframalpha.com/input/?i=1%2F%28x%2B1%29%E2%89%A52%2F%28x^2-1%29from-4to8
Die markierten Bereiche geben die Punktmengen an, für die die Ungleichung gilt. Auf der x - Achse kann man erkennen, dass die gefundene Lösung korrekt ist.