Aufgabe:
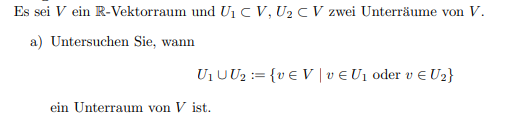
Text erkannt:
Es sei \( V \) ein \( \mathbb{R} \) -Vektorraum und \( U_{1} \subset V, U_{2} \subset V \) zwei Unterräume von \( V \).
a) Untersuchen Sie, wann
$$ U_{1} \cup U_{2}:=\left\{v \in V \mid v \in U_{1} \text { oder } v \in U_{2}\right\} $$
ein Unterraum von \( V \) ist.
Problem/Ansatz:
Hab schon ähnliche Aufgaben gesehen, aber die wussten schon, dass das gelten muss "wenn U1 ⊆ U2 oder U1 ⊇ U2 gilt"
Text erkannt:
Es sei \( V \) ein \( \mathbb{R} \) -Vektorraum und \( U_{1} \subset V, U_{2} \subset V \) zwei Unterräume von \( V \).
a) Untersuchen Sie, wann
$$ U_{1} \cup U_{2}:=\left\{v \in V \mid v \in U_{1} \text { oder } v \in U_{2}\right\} $$
ein Unterraum von \( V \) ist.
.