Funktionen: Berechnen von Schnittpunkten einer Parabel y=-x^2+6x-5 mit Gerade die durch A und B gehen

Question

Die Aufgabe ist aus der Rubrik Funktionen.

Berechnen Sie die Schnittpunkte der Parabel mit Funktion y=-x^2+6x-5

mit den Gerade, die durch die beiden Punkte A & B verlaufen / A(2/0) B(4/3)

Leider sind bei mir die Funktionen schon etwas weiter weg im Gedächnis, daher benötige ich  eure Hilfe.

Danke für Eure Unterstützung im Voraus

Answer 1

 

die Gerade, die durch A und B verläuft, hat die Steigung (3-0)/(4-2), also m = 3/2.

Geradengleichung allgemein

y = mx + b

Setzen wir m und die Koordinaten von A ein, erhalten wir

0 = 3/2 * 2 + b

-b = 3

b = -3

Damit lautet die Geradengleichung

y = 3/2 * x - 3

 

Um nun die Schnittpunkte mit der Parabel der Funktion

f(x) = - x² + 6x - 5

zu berechnen, müssen wir gleichsetzen:

 

3/2 * x - 3 = -x² + 6x - 5

-x² + 6x - 3/2 * x - 5 + 3 = 0

-x² + 9/2 * x - 2 = 0 | * (-1)

x² - 9/2 * x + 2 = 0

pq-Formel

x_1,2 = 9/4 ± √(81/16 - 32/16) = 9/4 ± √(49/16) = 9/4 ± 7/4

x₁ = 16/4 = 4 | y₁ = 3/2 * 4 - 3 = 3

x₂ = 2/4 = 1/2 | y₂ = 3/2 * 1/2 - 3 = 3/4 - 3 = 3/4 - 12/4 = - 9/4

 

Und so sieht das dann aus:

 

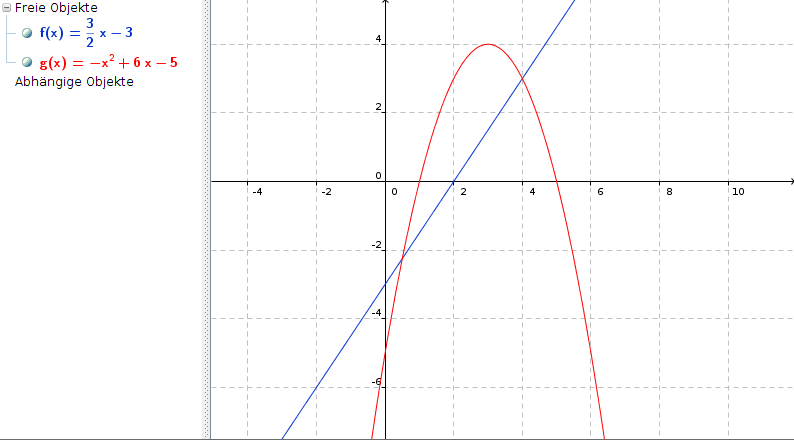
Besten Gruß

Answer 2

-x²+6x-5 |:-1

x² -6x +5 = 0 

 A(2/0) B(4/3)

Allgemeine Funktionsgleichung (Lineare Funktionen)

y= m*x + b     

Wir setzen beide Punkte in y = mx + b ein und lösen das lineare Gleichungssystem im Anschluss:

P1: 0= m*2 + b 

P2: 3= m*4 + b 

Wir stellen die erste Gleichung nach b um:

0= 2m + b | -2x

0 - 2m = b

Und setzen dies in die zweite Gleichung ein:

3= m*4 + b

3= 4m  + 0 -2m | -0

3= 2m                 | :2

m= 1,5 
 

Mit m = 1,5 gehen wir in die erste Gleichung:
 

0= m*2 + b 

0= 2*1,5 + b

0= 3 + b   | -3

-3 = b 

Mit b = 1 und m = 1 erhalten wir:

y=m*x +b 

y= 1,5x -3 

Gleichsetzen (Gleichsetzungsverfahren)

1,5x -3 = x² -6x + 5 | +6x

7,5x -3 = x² +5   | +3

7,5x    = 8  + x² | ...

Weiß hier leider nicht mehr weiter ...hoffe der rest hilft dir weiter, wenn etwas falsch ist, bitte korriegieren :)

Liebe Grüße

Emre 


 

Comments

neein, ich dachte vor  y=-x²+6x-5 also vor x² wäre eine Zahl und habe dann auch durch -1 geteilt :( 

Sorry da kommt: fx)= x²  + 6x - 5