Das war das vorherige Beispiel und händisch habe ich das überprüft und komme auch auf 0, sollte es jedoch nicht …

Question

Aufgabe:

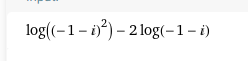
Text erkannt:

\( \log \left((-1-i)^{2}\right)-2 \log (-1-i) \)

Ich muss diesen Ausdruck in kartesischer Form darstellen und bin am verzweifeln..

Text erkannt:

Input:
\( \log \left((1+i)^{2}\right)-2 \log (1+i) \)
Result:
0

Problem/Ansatz:

So laut Wolframalpha sollte 2πi rauskommen, wenn ich es jedoch händisch rechne sprich zuerst in Polarkoordinaten etc komme ich immer wieder auf das Ergebnis 0.

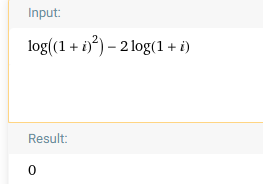
Text erkannt:

Input:
\( \log \left((1+i)^{2}\right)-2 \log (1+i) \)
Result:
0

Das war das vorherige Beispiel und händisch habe ich das überprüft und komme auch auf 0, sollte es jedoch nicht gleich wie das obige sein, da die Vorzeichen umgedreht sind? Ich bedanke mich im voraus für jeden Tipp!

Answer 1

Ist dir klar, dass der Logarithmus im komplexen periodisch ist?

Wolframalpha gibt dir eine von unendlich vielen Lösungen aus. Du hast händisch eine andere von unendlich vielen Lösungen ausgerechnet.

Comments

War mir nicht klar! Heißt das auch ich könnte händisch mit dem selben Ausdruck auf unendlich viele Lösungen stoßen?

---

(-1-i) hat den Betrag \( \sqrt{2} \) und das Argument \( \frac{5\pi}{4} \).

Die gleiche komplexe Zahl erhält man z.B. aber auch mit dem Argument \(2\pi+\frac{5\pi}{4} \).

Wenn du die vorkommenden komplexen Zahlen in Exponentialform schreibst und davon den Logarithmus bildest, bleiben nur die (komplexen) Exponenten übrig.