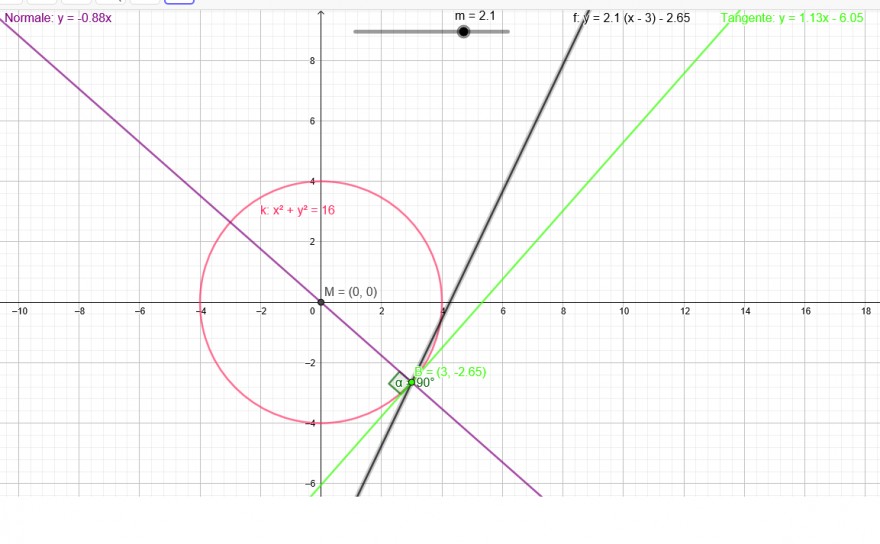
Zur Erklärung betrachte den Kreis k: x^2+y^2=16
Es soll nun eine Tangente an den Kreis in B(3|-2,65) konstruiert werden.
Das Geradenbüschel im Punkt B(3|-2,65) hat die Funktion:
\( \frac{y-(-2,65)}{x-3} \) = m
y = m • x - 3 m - 2,65
y = m• ( x - 3 ) - 2,65
Diese Geraden haben alle den Punkt B(3|-2,65) gemeinsam aber eine verschiedene Steigung. Schnittpunkte. Bei m=2,1 hast du 2 Schnittpunkte . (In der Zeichnung schwarz).
Bei einer Steigung von m=1,13 ist nur ein Berührpunkt da.
Bei der Tangente darf aber nur ein Schnittpunkt vorhanden sein.
Die Normale steht nun senkrecht auf der Tangente und läuft durch den Mittelpunkt des Kreises.
Eine Gerade durch M(0|0) und B(3|-2,65) hat die Steigung m_N= - 0,88
Es gilt m_T • m_N = - 1
Bezogen auf deine Aufgabe siehst du nun, dass du zuerst die Tangentensteigung bei der Nullstelle berechnen musst.
Die Normale in diesem Punkt geht dann durch den Mittelpunkt des Kreises.
Ich habe "GeoGebra" als Zeichnungsprogramm auf meinem PC.
mfG
Moliets