Partielle Ableitung 2. Ordnung mit ln

Question

Aufgabe:

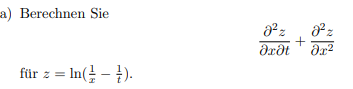
Text erkannt:

a) Berechnen Sie
$$ \begin{array}{l} \frac{\partial^{2} z}{\partial x \partial t}+\frac{\partial^{2} z}{\partial x^{2}} \\ \text { für } z=\ln \left(\frac{1}{x}-\frac{1}{t}\right) \end{array} $$

Problem/Ansatz:

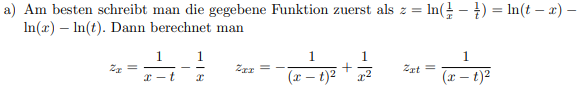
Text erkannt:

a) Am besten schreibt man die gegebene Funktion zuerst als \( z=\ln \left(\frac{1}{x}-\frac{1}{t}\right)=\ln (t-x)- \) \( \ln (x)-\ln (t) . \) Dann berechnet man
$$ z_{x}=\frac{1}{x-t}-\frac{1}{x} \quad z_{x x}=-\frac{1}{(x-t)^{2}}+\frac{1}{x^{2}} \quad z_{x t}=\frac{1}{(x-t)^{2}} $$

Ich rechne andauernd durch und bekomme für

zx = t/x(x-t)

zxx = - t(2x-t) / x^2(x-t)^2

und für zxt = 1/(x-t)^2

Ist die Lösung für zx und zxx nicht falsch oder ist das einfach anderst vereinfacht?

Answer 1

1. \( z_x \) auf den Hauptnenner bringen und vereinfachen, dann ist das Ergebnis das gleiche wie bei Dir.

2. \( z_{xx} \) das gleiche wie oben

3. \( z_{xt} \) passt ja.

Das ganze ergibt dann $$ z_{xt} + z_{xx} = \frac{1}{x^2} $$