Hallo,
um den Strahlensatz anzuwenden benötigst Du zwei Parallelen. Die sind bei Dir oben nicht eingezeichnet. Ich postuliere mal, dass \(x\) und die \(2,5\) senkrecht auf der Waagerechten stehen. Dann ergibt sich folgendes Bild:
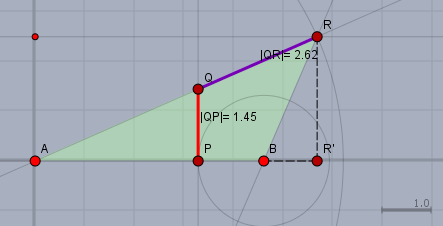
Berechne zunächst die Strecke \(|AR'|\) nach dem Pythagoras$$|AR'| = \sqrt{|AR|^2 - |RR'|^2} \approx 5,674$$weiter ist $$|AP| = |AB| - |PB| = 3,28$$nach dem Strahlensatz ist $$\frac{x}{|AP|} = \frac{|RR'|}{|AR'|} \\ \implies x = \frac{|RR'|}{|AR'|} \cdot |AP| = \frac{2,5}{5,674} \cdot 3,28 \approx 1,45$$ und die Strecke \(y\) solltest Du nun allein schaffen.
Falls nicht, so frage nochmal nach.
Gruß Werner