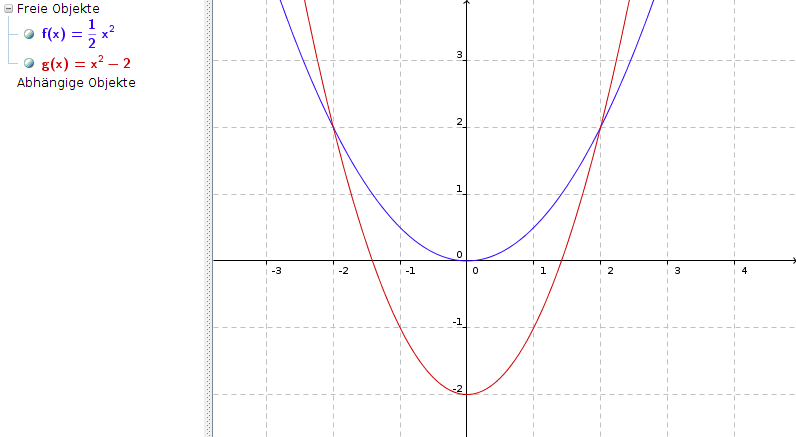
p1: f(x) = ax2
p2: g(x) = x2 + c
Sie haben P(2|2) gemeinsam, also setzen wir x = 2 und y = 2 in die beiden Funktionsgleichungen ein:
f(2) = a * 22 = 2 | also a = 2/4 = 1/2
f(x) = 1/2 * x2
g(2) = 22 + c = 2 | also c = 2 - 4 = -2
g(x) = x2 - 2
Besten Gruß