Text erkannt:
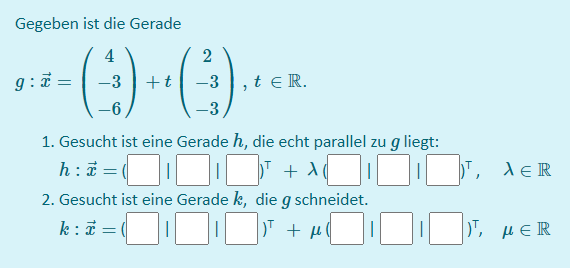
Gegeben ist die Gerade
\( g: \vec{x}=\left(\begin{array}{c}4 \\ -3 \\ -6\end{array}\right)+t\left(\begin{array}{c}2 \\ -3 \\ -3\end{array}\right), t \in \mathbb{R} \)
1. Gesucht ist eine Gerade \( h \), die echt parallel zu \( g \) liegt:
2. Gesucht ist eine Gerade \( k \), die \( g \) schneidet.
Gegeben ist die Gerade
\( g: \vec{x}=\left(\begin{array}{c}4 \\ -3 \\ -6\end{array}\right)+t\left(\begin{array}{c}2 \\ -3 \\ -3\end{array}\right), t \in \mathbb{R} \)
1. Gesucht ist eine Gerade \( h \), die echt parallel zu \( g \) liegt:
2. Gesucht ist eine Gerade \( k \), die \( g \) schneidet.
Kann mir jemand, wenn möglich, bei der Lösung helfen?