∫03 |2x2-6x| dx = |[2/3*x3 - 3x2]03| bin soweit gekommen, aber komme hier nicht mehr weiter ^^ help

Question

∫₀³ |2x²-6x| dx = |[2/3*x³ - 3x²]₀³|  so sollte s eigentlich weiter gehen -->  = |18 - 27| = |-9| = 9 

aber ich weiß nicht, wie man auf 18-27 kommt? und wieso macht man da immer diese | dinger? 

danke für eurere Antworten, bald habe ich es endgültig verstanden!

PS: ich bin noch nicht auf der Oberstufe, ich lerne das aus Interesse ^^) aber bald bin ich auf der Obersufe :)

Answer 1

Hallo Emre,

 

diese Dinger | heißen Betragsstriche, und die setzt man, damit man keine negativen Flächeninhalte bekommt :-)

Zum Beispiel:

|5| = |-5| = 5

 

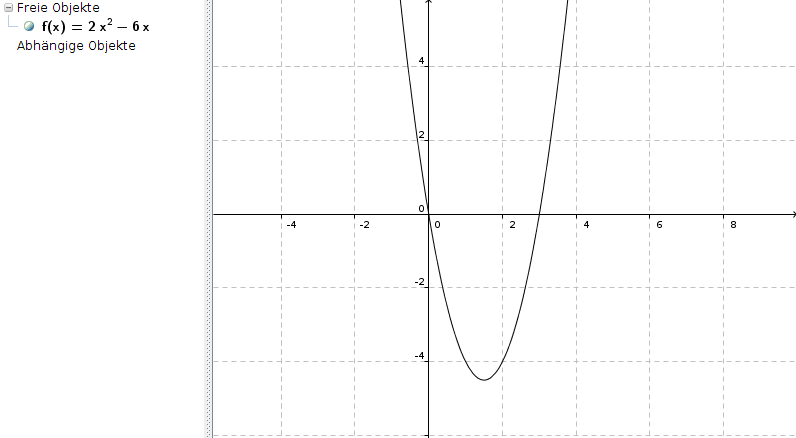
∫₀³ |2x²-6x| dx = |[2/3*x³ - 3x²]₀³|

Bis hierhin ist ja alles richtig.

Nun setzt Du die obere Grenze Deines Integrals, also die 3 in den Ausdruck in eckigen Klammern ein

2/3 * 3³ - 3 * 3²

und subtrahierst davon den Ausdruck in eckigen Klammern, in den Du die untere Grenze 0 eingesetzt hast

2/3 * 0³ - 3 * 0²

Dieser zweite Teil ist offensichtlich = 0, also bleibt nur

 

|2/3 * 3³ - 3 * 3²| = |2/3 * 27 - 3 * 9| = |18 - 27| = |-9| = 9

 

Wie gut, dass wir die Betragsstriche gesetzt haben, sonst hätten wir jetzt eine Fläche von -9 raus :-)

Und zwar deshalb:

Besten Gruß

Comments

Hallo Brucybabe :)

Danke auch für deine sehr gute Antwort!! Allerdings weiß ich jetzt nicht, wem ich den Stern geben soll :(

Du und Unknown seit meine Lieblingsuser auf Gute Mathe Fragen :)

es fehlt mir so schwer :(

---

Machs Dir nicht so schwer. Seine Antwort ist ausführlicher und sauberer. Der Sternträger damit klar definiert ;).

Zudem bin ich damit zufrieden, wenn Du Verständnis signalisierst! Das ist wichtiger als ein paar Punkte/Sterne.

---

Na dann ok:) :)) supii:)

---

@Emre:

Vielen Dank für den Stern :-)

@Unknown:

Das ist wie immer sehr freundlich von Dir!

@beide:

Da kann ich mich nur mit zwei kleinen Däumchen bedanken :-D

Answer 2

Hi Emre,

Deine Aufgabe ist es nun die Grenzen einzusetzen.

|[2/3*x³ - 3x²]₀³|

D.h.

(2/3 * 3^3 - 3*3^2) - (2/3*0^3 - 3*0^2) = |2/3*27 - 3*9| = |18-27| = 9

 

Klar?

Grüße

Comments

Sehr empfehlenswert für etwas mehr Informationen:

http://www.brinkmann-du.de/mathe/gost/int_01_03.htm

---

Jap, jetzt ist es klar :) danke Unknown!!!!!!!!!!!!!!!!!!!!!!!! Ich mache dann nochmal eine andere Aufgabe, kannst du sie dann gucken, ob es stimmt? bittttttttteee also ich poste es wieder als eine neue Frage :)

---

Wenn sie im Bereich meiner Fähigkeiten liegt, schaue ich gerne drüber :).

Freut mich, das obiges verstanden wurde.

P.S.: Brinkmann halte ich übrigens für eine schöne Seite. Wenn Dir langweilig ist, kannste da auch ab und an mal reinschauen ;).