Aufgabe:
Das graue Rechteck wird gedreht, so dass jeweils ein weißes Rechteck entsteht. Geben sie die Zugehörige (2,2)-Matrix A1 an, die die Liberale Abbildung beschreibt.
Das Rechteck hat die Eckpunkte:
P1(-1|0) , P2(2|0) , P3(2|2) , P4(-1|2)
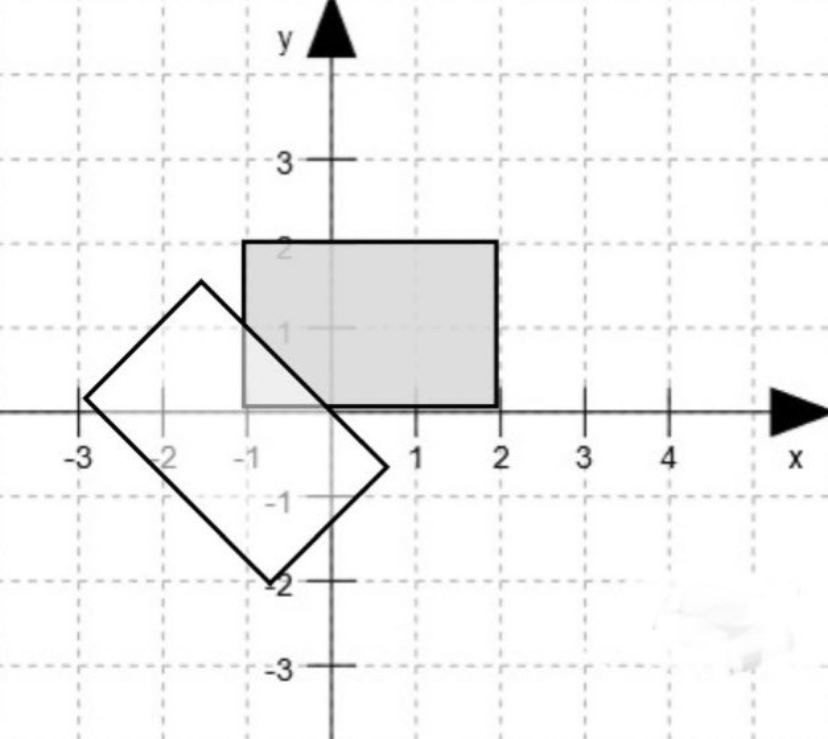
Das neue Rechteck ist um 45 grad im Uhrzeigersinn gedreht. Ich muss höchstwahrscheinlich hier mit der drehmatrix an die Aufgabe dran, jedoch fehlt mir jeglicher Ansatz.
Hoffe Ihr habt ein paar Tipps für mich. Vielen Dank.