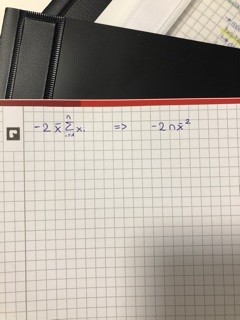Probleme beim finden des Rechenwegs der Summe

Question

Hallo,

ich bin gerade dabei, etwas zu beweisen.

Dabei bin ich bei folgendem ins Stocken geraten.

Ichmöchte die linke Seite in die Rechte führen, ich weiß das es der letzte Schritt ist aber ich weiß nicht wie ich das rechnen müsste.

Kann mir jemand bei dem Rechenweg helfen?

Liebe Grüße :)

Comments

Was für x_i sind das?

Answer 1

Aloha :)

$$2\overline x\sum\limits_{i=1}^nx_i=2\overline x\cdot n\cdot\underbrace{\frac{1}{n}\sum\limits_{i=1}^nx_i}_{=\overline x}=2\overline x\cdot n\cdot\overline x=2n\,\overline x^2$$

Comments

Wieso darf ich denn einfach mit n•x(strich) multiplizieren?

Also welche Regel ist das denn?

---

Hat sich erledigt , war eine blöde frage ☺

---

Ich habe nichts addiert, sondern eine "nahrhafte" \(1\) in der Form:$$n\cdot\frac{1}{n}=1$$eingebaut. Damit wird dann:$$2\overline x\cdot\sum\limits_{i=1}^nx_i=2\overline x\cdot1\cdot\sum\limits_{i=1}^nx_i=2\overline x\cdot \underbrace{n\cdot\frac{1}{n}}_{=1}\cdot\sum\limits_{i=1}^nx_i$$$$=2\overline x\cdot n\cdot\underbrace{\left(\frac{1}{n}\cdot\sum\limits_{i=1}^nx_i\right)}_{=\overline x}=2\overline x\cdot n\cdot\overline x=2n\,\overline x^2$$

Answer 2

Wenn das so stimmt, dann müsste die Summe selbst gerade n\(\overline{x}\) ergeben.