"Aufgabe 4. Der Graph einer ganzrationalen Funktion dritten Grades geht durch den Koordinatenursprung und hat in S(-1|-1/3) einen Sattelpunkt. Wie lautet die Funktion?"
Ich verschiebe den Graphen um 1/3 nach oben S´(-1|0) Da der Graph durch den Ursprung verlaufen soll, ergibt dies einen neuen Punkt P(0|1/3):
f(x)=a*(x+1)^3
P(0|1/3)
f(0)=a*(0+1)^3
a*(0+1)^3=1/3
a=1/3
f(x)=1/3*(x+1)^3
Nun wieder um 1/3 nach unten verschieben:
p(x)=1/3*(x+1)^3-1/3
mfG
Moliets
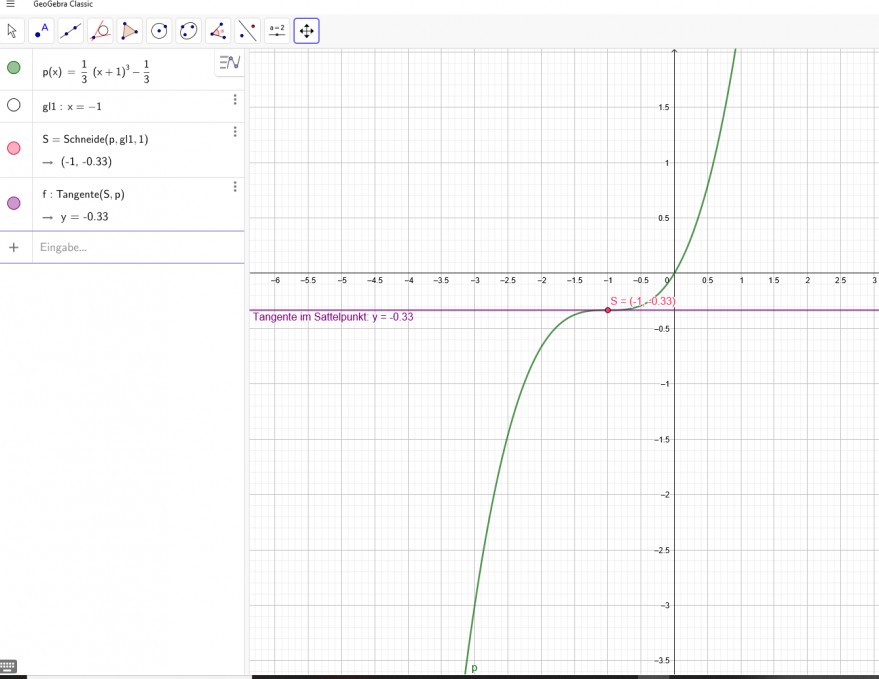
Text erkannt:
\( p(x)=\frac{1}{3}(x+1)^{3}-\frac{1}{3} \)
\( g \mid 1: x=-1 \)
\( \mathrm{S}= \) Schneide \( (\mathrm{p}, \mathrm{g} 11,1) \)
\( \rightarrow(-1,-0.33) \)
f: Tangente(S, p)
\( \rightarrow y=-0.33 \)
Eingabe...