Machen wir mal ein Beispiel:
Ein Kegel mit Höhe 10 und Grundflächenradius 5 steht auf dem Ursprung. Dadurch verläuft die Ebene y - 25z = -125.
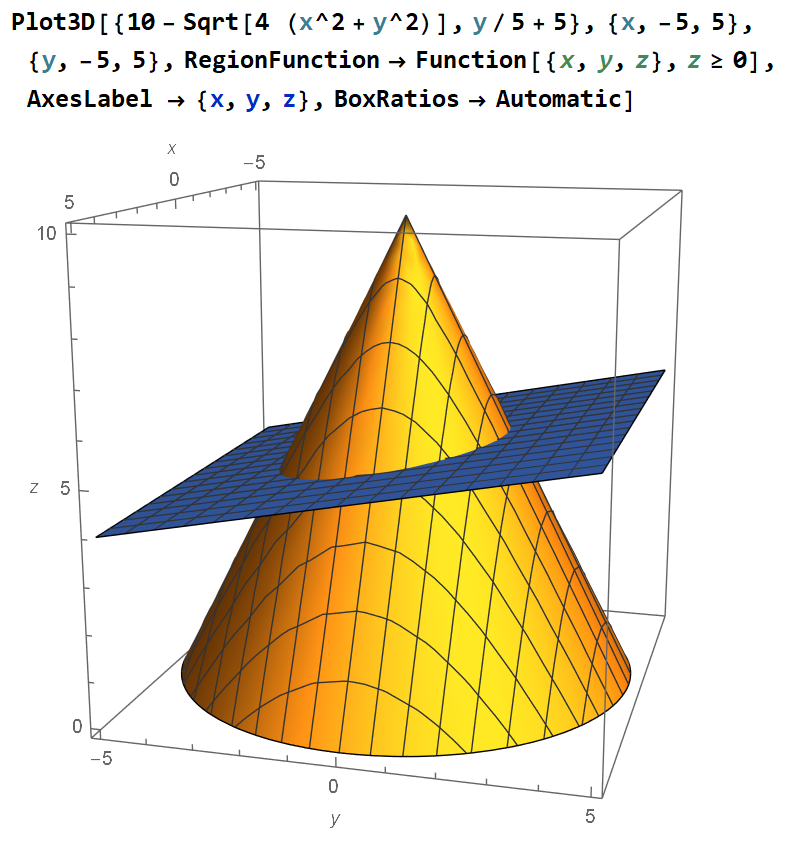
Wenn man die beiden Flächen gleichsetzt hat man die Ellipse \( 10 \sqrt{x^{2}+y^{2}}+y=25 \), und auf der sucht man dann das minimale und maximale z. In diesem Beispiel ist das dort, wo x = 0.