f_a(x)=a / 6 *[ x^3 - (5+a )* x^2 +(4+5*a)*x-4a]
a / 6 *[ x^3 - (5+a )* x^2 +(4+5*a)*x-4a]=0
x^3 - (5+a )* x^2 +(4+5*a)*x-4a=0
f_a(x)= x^3 - (5+a )* x^2 +(4+5*a)*x-4a
f_1(x)= x^3 - 6* x^2 +9*x-4
f_2(x)= x^3 - 7 x^2 +14*x-8
x^3 - 6* x^2 +9*x-4= x^3 - 7 x^2 +14*x-8
x^2 -5x= -4
(x-2,5)^2=2,25
x_1=2,5+1,5=4
x_2=2,5-1,5=1
Somit sind 4 und 1 von a unabhängige Nullstellen.
Berechne nun die von a abhängigen Nullstellen. 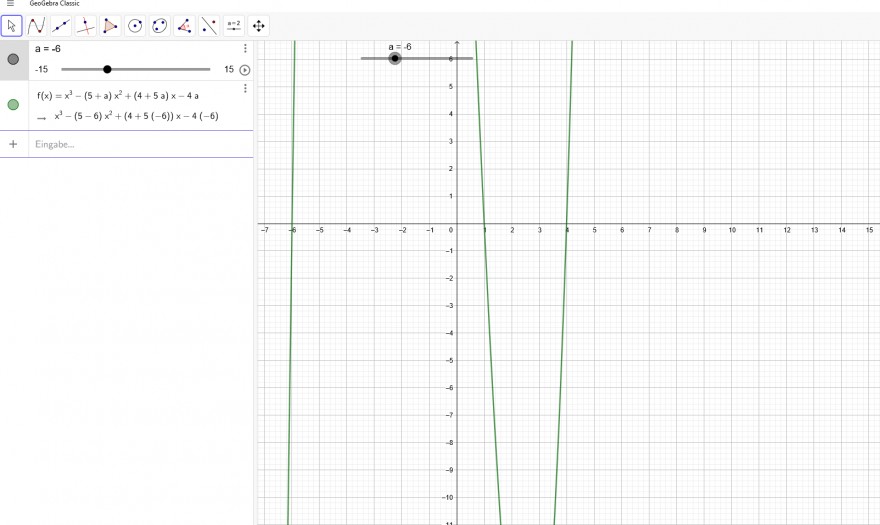
Text erkannt:
R) \( 0<\cdots=4 \)
\begin{tabular}{c}
\( { }^{3}-(5-6) x^{2}+(4+5(-6)) \times-4(-6) \) \\
\hline
\end{tabular}
mfG
Moliets