Polynomfunktionen Polynomdivision Hilfe

Question

Aufgabe

Aufgabe Gegeben ist die Funktion \( f_{3}(x)=x^{4}-9 x^{3}+20 x^{2}+5 x-25 \) Zeige zunächst, dass \( x_{1}=-1 \) und \( x_{2}=5 \) zwei Nullstellen der Funktion \( f_{3}(x) \) sind, finde anschliessend alle weiteren Nullstellen und skizziere den Graphen!(1) \( f_{3}(x)=x^{4}-9 x^{3}+20 x^{2}+5 x-25:(x+1)=x^{3}-10^{2}+30 x-25 \)

Text erkannt:

Aufgabe Gegeben ist die Funktion \( f_{3}(x)=x^{4}-9 x^{3}+20 x^{2}+5 x-25 \) Zeige zunächst, dass \( x_{1}=-1 \) und \( x_{2}=5 \) zwei Nullstellen der Funktion \( f_{3}(x) \) sind, finde anschliessend alle weiteren Nullstellen und skizziere den Graphen!
(1) \( f_{3}(x)=x^{4}-9 x^{3}+20 x^{2}+5 x-25:(x+1)=x^{3}-10^{2}+30 x-25 \)

Problem/Ansatz:

Ich komme leider nicht mehr weiter.

Answer 1

f(x) = x^4 - 9·x^3 + 20·x^2 + 5·x - 25

Horner Schema bei x = 5

1	-9	20	5	-25
0	5	-20	0	25
1	-4	0	5	0

Weil 0 heraus kommt ist x = 5 eine Nullstelle und x^3 - 4x^2 + 5 ist das Restpolynom

Horner Schema bei x = -1

1	-4	0	5
0	-1	5	-5
1	-5	5	0

Weil 0 heraus kommt ist x = -1 eine Nullstelle und x^2 - 5x + 5 ist das Restpolynom

x^2 - 5x + 5 = 0 --> x = 5/2 ± √5/2 --> x = 1.381966011 ∨ x = 3.618033988

Skizze

~plot~ x^4-9x^3+20x^2+5x-25;[[-6|6|-30|20]] ~plot~

Answer 2

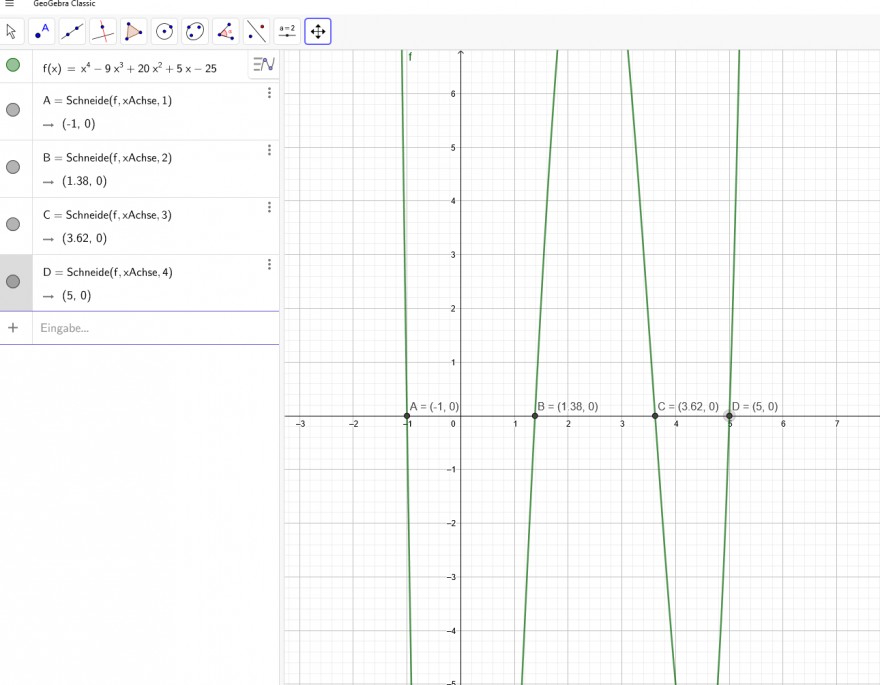
f(x)=x^4-9x^3+20x^2+5x-25

x₁=  -1   Nullstelle von f(x)=x^4-9x^3+20x^2+5x-25

f(-1)=(-1)^4-9*(-1)^3+20*(-1)^2+5*(-1)-25

(-1)^4- 9*(-1)^3+ 20*(-1)^2+ 5*(-1)-25 = ?0

1+9+20-5-25=0  → Stimmt somit

x₂=5   Nullstelle von f(x)=x^4-9x^3+20x^2+5x-25

f(5)=5^4-9*5^3+20*5^2+5*5-25

5^4- 9*5^3+ 20*5^2 + 5*5- 25 = ?0

5^4-9*5^3+20*5^2+5*5-25=0 → Stimmt somit

Polynomdivision:

(x^4-9x^3+20x^2+5x-25):[(x+1)*(x-5)]=

=(x^4-9x^3+20x^2+5x-25):(x^2-4x-5)=x^2-5x+5

x^2-5x+5=0

x₁= 2,5+ 1/2*\( \sqrt{5} \) ~~3,62

x₂= 2,5 - 1/2*\( \sqrt{5} \) ~~1,38