f(x) = 0,27x2 * e-0,12x
Produktregel (uv)' = u'v + uv'
u = 0,27x2
u' = 0,54x
v = e-0,12x
v' = -0,12 * e-0,12x
f'(x) = 0,54x * e-0,12x + 0,27x2 * (-0,12) * e-0,12x = (0,54x - 0,0324x2) * e-0,12x
Der zweite Faktor wird niemals = 0.
-0,0324x2 + 0,54x = 0
x * (-0,0324x + 0,54) = 0
x1 = 0
-0,0324x + 0,54 = 0
x2 = 0,54/0,0324 = 16 2/3 = 50/3
Jetzt müsste man noch überprüfen, ob die 2. Ableitung der Funktion für x1 = 0 bzw. für x2 = 50/3 ungleich 0 ist.
Für Werte > 0 erhält man ein Minimum, für Werte < 0 ein Maximum.
Außerdem muss man 0 bzw. 50/3 in die Ursprungsfunktion einsetzen, um die entsprechenden y-Werte zu erhalten.
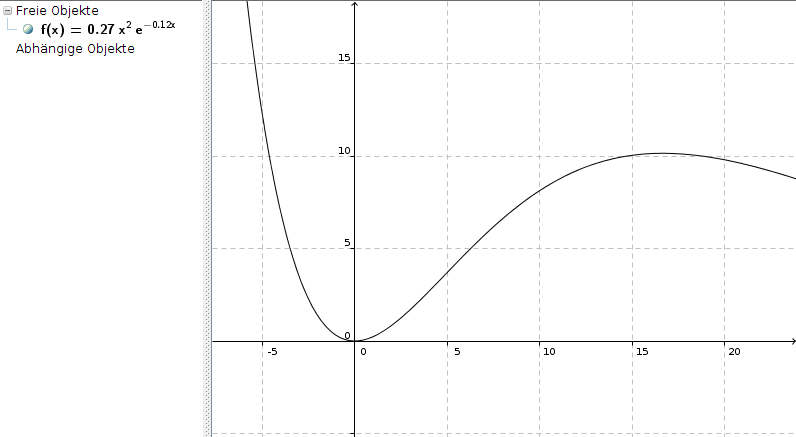
Wir haben hier ein Minimum an der Stelle 0 und ein Maximum an der Stelle 50/3:
Besten Gruß