Art und Lage eines Kegelschnittes, Aufstellen der Ortskurve

Question

Ich hab hier ein kleines problem mit einer kegelschnittaufgabe ich hoffe ihr könnt mir helfen ;)

der eckpunkt B des dreiecks OAB mit O(0/0) und A(7/0) bewegt sich auf der kurve k: x^2+y^2-6x-8y=-16

a) klassifizieren sie die kurve hinsichtlicht art und lage

b) auf welcher ortskurve liegen die mittelpunkte M der dreiecksseiten (Gleichung und Klassifikation)

a) Kegelschnittgleichung:  Ax^2+By^2+Cx+Dy+E=0

A=B also ist es ein Kreis
mit der hauptform (kreis in allg. lage) kann man dann den mittelpunkt und den radius bestimmen.

(x-xo)^2+(y-yo)^2=r^2

x^2-2xxo+xo^2+y^2-2yyo+yo^2=r^2

-2xxo = -6x  xo=3

-2yyo = -8y  yo=4

M(3/4)

x^2+y^2-r^2 = c

9+16-r^2 = 16

r=3

Mein problem ist nun  1. ich hab null ahnung ob a) stimmt

                                        2. ich weiß nicht wie ich nun bei b) die ortskurve aufstellen kann

Answer 1

Kreis:

x^2+y^2-6x-8y=-16

x^2-6x+9+y^2-8y+16=9

(x-3)^2+(y-4)^2=9

M(3|4)  r=3

Der Eckpunkt B des Dreiecks OAB mit O(0|0) und A(7|0) bewegt sich auf der kurve k: x^2+y^2-6x-8y=-16

Ich verschiebe den Graph um 4 Einheiten nach unten und 3 Einheiten nach links:

Kreis: x^2+y^2=9     O´(-3|-4)    A´(4|-4)

y=-\( \sqrt{9-x^2} \)    und y=\( \sqrt{9-x^2} \)

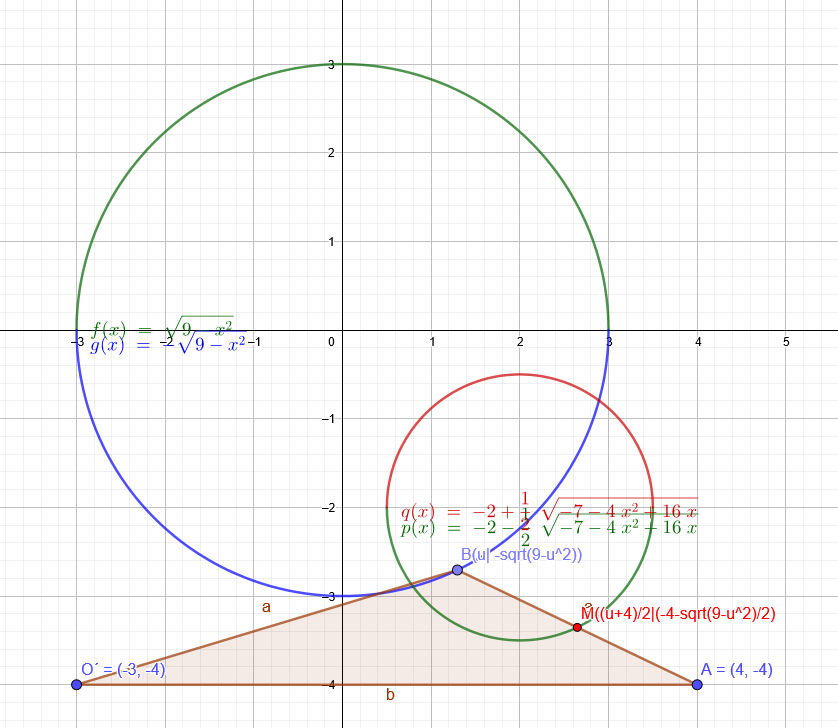
Ortslinie:
\( x=\frac{u+4}{2} \rightarrow \rightarrow u=2 x-4 \in y \) einsetzen
\( y=\frac{-4-\sqrt{9-u^{2}}}{2} \)
\( y=\frac{-4-\sqrt{9-(2 x-4)^{2}}}{2}=\frac{-4-\sqrt{-7-4 x^{2}+16 x}}{2}=-2-\frac{1}{2} \cdot \sqrt{-7-4 x^{2}+16 x} \)
\( 2 .) y=-2+\frac{1}{2} \cdot \sqrt{-7-4 x^{2}+16 x} \)

Nun alles wieder verschieben.