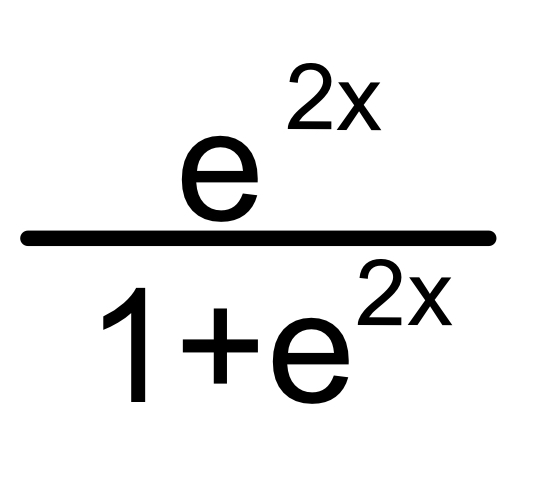
Text erkannt:
\( \frac{e^{2 x}}{1+e^{2 x}} \)
Berechnen Sie den Inhalt der Fläche A unter dem Graphen von f über dem Intervall I.
c) f(x)=e^(2*x)/(e^(2*x)+1) , I=[10,11]
Problem/Ansatz:
Ich weiß, dass ich die Funktion integrieren muss und die Grenzen in die Stammfunktion einsetzen muss.
Aber ich verstehe nicht, wie man die Stammfunktion von f(x) bilden soll?