Question

Weiß jemand mit welchen methoden man diese Gleichungen lösen kann?

a) x^2-20=5

b) 2x^2+4x+3=0

c) 6x^6-4x^3+14=0

d)\( \frac{4}{7} \)x+\( \frac{6}{8} \)=42

ich habe bei a) Äquivalenzumformung

bei b) PQ formel

und bei c) und d) hab ich keine ahnung

gibt es für die ersten zwei noch mehr?

Comments

Die Gleichungen a) und b) sind quadratisch. Da geht die Mitternachtsformel immer.

Die Gleichung c) hat keine Lösung in den reellen Zahlen. Wenn Du d) nicht lösen kannst, dann kennst Du auch (noch) keine Methode, um c) zu lösen. Du kannst dem Plot der Funktion entnehmen, dass sie nirgends gleich Null wird:

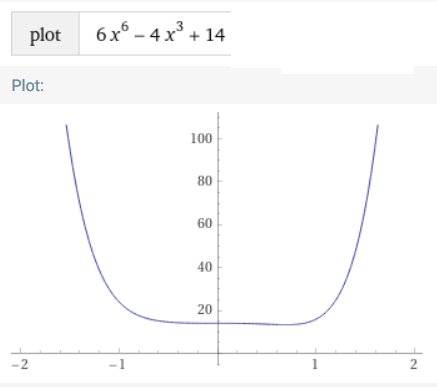
Bei d) subtrahierst Du auf beiden Seiten 6/8 und dividierst dann durch 4/7.

Answer 1

Hallo,

a) x^2-20=5 |+20

x^2=25

x1.2=±5

b) 2x^2+4x+3=0 |:2

x^2+2x+3/2=0  ->z.b pq-Formel

x1.2=-1± √(1-(3/2)

x1.2=-1± √-1/2

x1.2=-1± i 1/√2

c )6x^6-4x^3+14=0

z=x^3

6 z^2 -4z -14=0|: 6

z^2 -(2/3)z -(7/3)=0 ->z.b pq-Formel

zum Schluß resubstituieren

d)

(4/7) x +6/8=42

(4/7) x +3/4=42 |-3/4

(4/7) x = 165/4

x=1155/16