Aufgabe:
Gegeben ist die folgende Dichtefunktion einer stetigen Zufallsvariable X
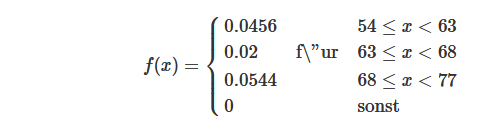
Text erkannt:
\( f(x)=\left\{\begin{array}{lll}0.0456 & & 54 \leq x<63 \\ 0.02 & \mathrm{f} \backslash \text { "ur } & 63 \leq x<68 \\ 0.0544 & & 68 \leq x<77 \\ 0 & & \text { sonst }\end{array}\right. \)
Berechnen Sie die Wahrscheinlichkeit P(61≤X≤74)
. (Geben Sie das Ergebnis in Prozent an.)
Problem/Ansatz:
Ich habe mich an einer ähnlichen Aufgabe die hier gelöst wurde orientiert und versucht die Aufgabe folgendermaßen zu lösen:
0,0456*(63-61)+0,02*(74-63)=0,03112=31,12%
Das hat leider nicht gestimmt. Jetzt habe ich hier eine andere Lösung gefunden und würde auf folgendes Ergebnis kommen:
0,0456*(63-61)+0,02*(69-63)+0,0544*(77-74)=0,03544=35,44%
Es wäre super, wenn mir jemand sagen könnte ob das stimmt.