Hallo Vroni,
schau Dir folgendes Bild an:
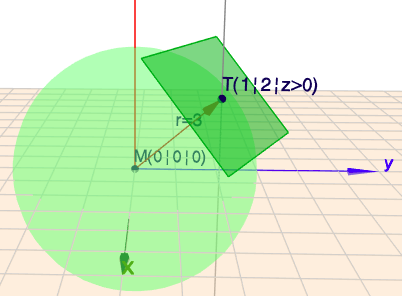
Die senkrechte Gerade (grau) enthält alle Punkt, mit einer x-Koordinate von 1 und einer y-Koordinate von 2. Also alles mögliche Kandidaten für \(T(1|2|z)\). Mit der zusätzlichen Bedingung, dass \(T\) auf der Kugelobefläche liegen soll, kommen nur die zwei Punkte in Frage, in denen die Senkrechte die Kugeloberfläche schneidet.
Nun zeichnet sich jeder Punkt auf der Kugeloberfläche dadurch aus, dass sein Abstand vom Mittelpunkt gleich dem Radius ist, hier \(r=3\). Das gilt auch für \(T\). Also muss gelten:$$|MT| = 3, \quad \implies (T-M)^2 = 3^2 \\ \begin{aligned}\implies (1-0)^2 + (2-0)^2 + (z-0)^2 &= 3^2 \\ 1 + 4 + z^2 &= 9 \\ z^2 &= 4 \\ z &= 2 &|\, \text{wg.} \space z \gt 0\end{aligned}$$die negative Lösung für \(z\) entfällt lt. Aufgabenstellung.
Zur Kontrolle: die Ebenengleichung ist$$E: \quad \begin{pmatrix}1\\ 2\\ 2\end{pmatrix} \vec x = 9$$Gruß Werner