Berechnen Sie den Inhalt der Fläche, die vom Graph von f, der Normalen in P und der x-Achse begrenzt wird.

Question

Die Normale im Punkt P auf dem Graphen einer Funktion f steht senkrecht zur Tangente in P (Fig.4). D.h.es gilt: Wen m die Steigung Dr Tangente in P ist, dann ist -1/m die Steigung der Normalen in P.

a) Berechnen Sie den Inhalt der Fläche, die vom Graph von f, der Normalen in P und der x-Achse begrenzt wird.

(1) f (×) = -×2; P (1/-1)  (2) f (×)=×3; P (1/1)

b) Berechnen Sie den Inhalt der Fläche, die vom Graphen der Funktion h mit h (×)=-×3+× und der Normalen im Wendepunkt von h eingeschlossen wird.

Comments

Graph der Funktion (Fig.4)

Answer 1

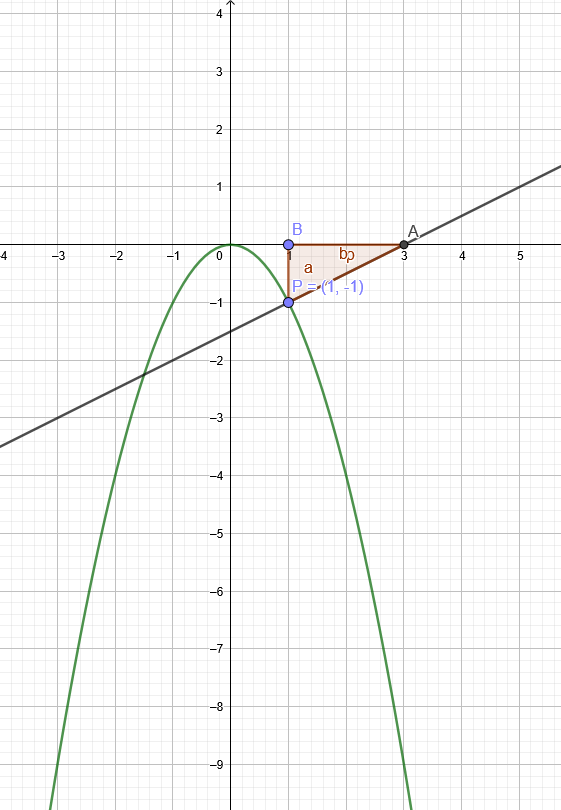
a) Berechnen Sie den Inhalt der Fläche, die vom Graph von f, der Normalen in P und der x-Achse begrenzt wird.

f (x) = - x^2  ;   P (1|-1)          

Berechnung der Normalen:

f´( x )= -2 x

f´( 1 )= - 2  das wäre die Tangentensteigung

Normalensteigung ist dann m_N= \( \frac{1}{2} \)

Gleichung der Normalen

\( \frac{y+1}{x-1} \)  = \( \frac{1}{2} \)

y = \( \frac{1}{2} \) x - \( \frac{3}{2} \)

Nullstelle: N( 3|0)

Fläche des Dreiecks A B P A_1=1 F E

Fläche über der Parabel:

A_2= Integral -x^2*dx im Intervall 0 bis 1→ [ -\( \frac{x^3}{3} \) ]=-\( \frac{1}{3} \) -0

A_2=\( \frac{1}{3} \) FE

Gesamtfläche 1F E+1/3F E = \( \frac{4}{3} \) F E

Comments

Super!Vielen Dank!

Ich habe es verstanden

Answer 2

Hallo

 1. f'(x) bilden, dann Normale  n(x) Bestimmen in P (x1,y1)  also Gerade mit Steigung m=-1/f'(x1)

Nullstelle von Normale und f(x) bestimmen,  dann Betrag des Integrals von f(x)-n(x) bestimmen-.

in b) erst den Wendepunkt mit f''=0 bestimmen, dann wie in a)

(eine Skizze der Funktion oder ein Plot hilft immer beim Verstehen der Aufgabe.)

Gruß lul

Comments

Dankeschön für die schnelle Antwort!