gegeben:
A (2 | 1 | -2) , v(Pfeil drüber)= (-4 | 2 | 4)
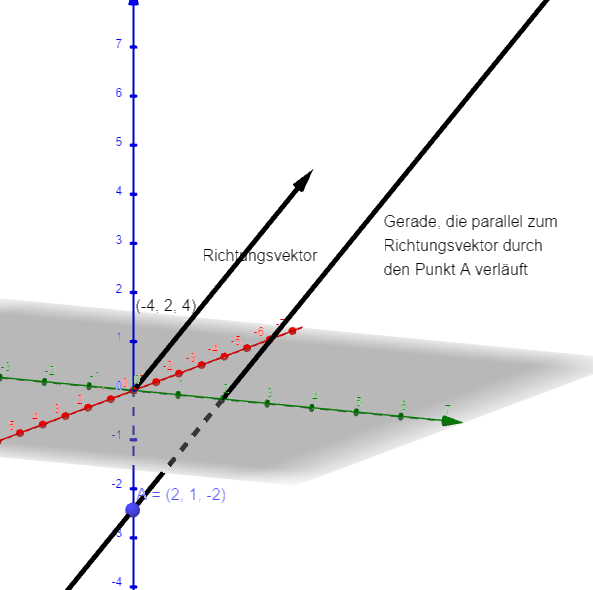
A ist ein Punkt, \( \vec{v} \) ist der Richtungsvektor, der angibt, in welche Richtung die Gerade g durch den Punkt A verläuft.
Wenn Punkt und Richtungsvektor gegeben sind, stellst du die Geradengleichung immer so auf:
g: \( \vec{x} \) =\( \vec{a} \) + \(r\cdot \vec{v}\)
\( \vec{a} \) = Koordinaten des (Anbindungs-)Punktes
r Parameter, der auch durch einen anderen Buchstaben dargestellt werden kann
\( \vec{v} \) Koordinaten des Richtungsvektors
Hast du das soweit verstanden?