Aufgabe:
Wieso konvergiert diese Zahlenfolge nicht gegen 1/4?
Problem/Ansatz:
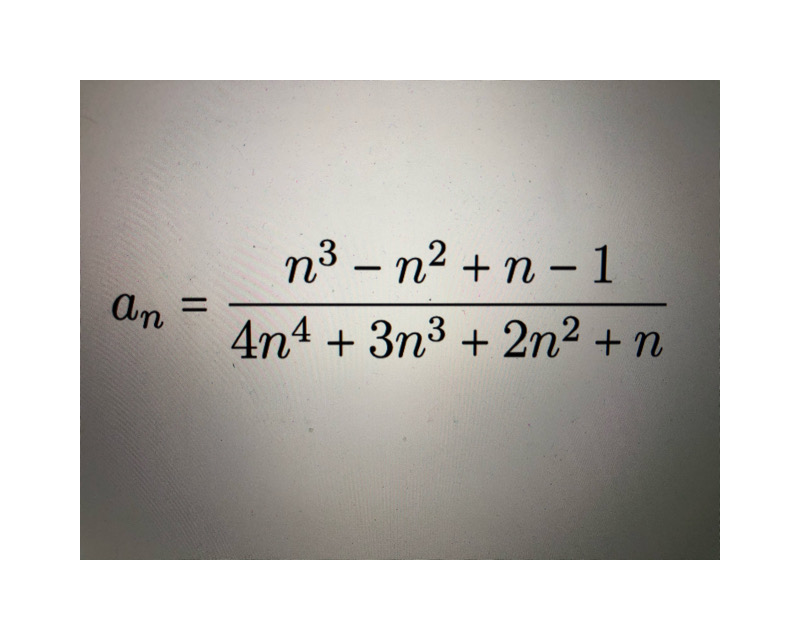
Ist dies vielleicht so weil der höchste Exponent im Nenner nicht derselbe ist wie im Zähler?
Wenn beides n^4 wäre, dann würde dies stimmen?
Danke für die Hilfe!
Text erkannt:
\( a_{n}=\frac{n^{3}-n^{2}+n-1}{4 n^{4}+3 n^{3}+2 n^{2}+n} \)