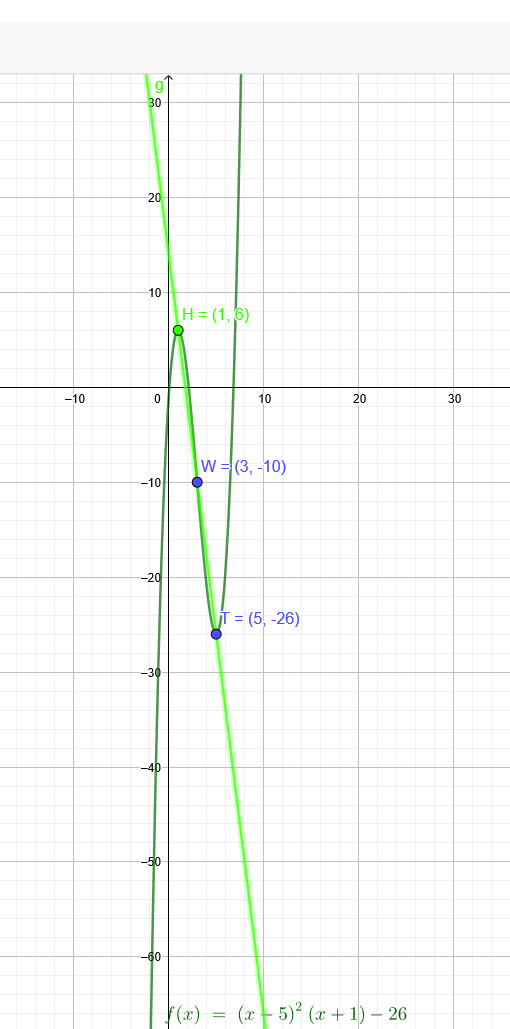
"Vom Graphen einer ganzrationalen Funktion 3. Grades sind der Wendepunkt W(3;-10) und der lokale Minimumpunkt T(5;-26) bekannt, und ich soll daraus jetzt eine Funktionsgleichung machen."
Ich verschiebe den Graphen um 26 Einheiten nach oben:
Wendepunkt W_1(3|16)
lokale Minimumpunkt T_1(5|0) → Nullstellenform der Parabel 3.Grades f_1(x)=a*(x-5)^2*(x-N)
f_1(3)= a*(3-5)^2*(3-N) = 4a*(3-N)
1.) 4a*(3-N) =16 → a*(3-N) =4 → a = \( \frac{4}{3-N} \)
f_1(x)=\( \frac{4}{3-N} \) *[(x-5)^2*(x-N) ]
[\( \frac{4}{3-N} \) * [(x-5)^2*(x-N) ]´=\( \frac{4}{3-N} \) *[2*(x-5)*(x-N)+(x-5)^2*1] =\( \frac{4}{3-N} \) *[(2x-10)*(x-N)+(x-5)^2]
[\( \frac{4}{3-N} \) *[(2x-10)*(x-N)+(x-5)^2]´=\( \frac{4}{3-N} \) *[2*(x-N)+(2x-10)*1+2(x-5)*1]
W_1(3|16)
\( \frac{4}{3-N} \) *[2*(3-N)+(2*3-10)+2(3-5)]=0
N= - 1
a = \( \frac{4}{3+1} \)= \( \frac{4}{4} \)=1
f_1(x)=(x-5)^2*(x+1)
f(x)=(x-5)^2*(x+1)-26
(Eine Besonderheit zeigt die grüne Linie. Welche?)
mfG
Moliets