Aloha :)
Die Summenformel für die unendliche geometrische Reihe lautet:$$\sum\limits_{k=0}^\infty x^k=\frac{1}{1-x}\quad;\quad |x|<1$$Setzen wir an Stelle von \(x\) einfach \((-x)\) ein, erhalten wir:$$\sum\limits_{k=0}^\infty (-x)^k=\frac{1}{1-(-x)}=\frac{1}{1+x}\quad;\quad |x|<1$$Da die Konvergenz der Reihe für \(|x|<1\) gesichert ist, können wir beide Seiten der Gleichung integrieren und in der Reihe alle Summanden einzeln integrieren:
$$\int\limits_0^x\sum\limits_{k=0}^\infty(-x')^k\,dx'=\int\limits_0^x\frac{1}{1+x'}\,dx'\quad\implies\quad\sum\limits_{k=0}^\infty\int\limits_0^x(-x')^k\,dx'=\left[\ln|1+x'|\right]_{x'=0}^x$$$$\ln(1+x)=\sum\limits_{k=0}^\infty-\frac{(-x)^{k+1}}{k+1}=\sum\limits_{k=1}^\infty-\frac{(-x)^{k}}{k}=\sum\limits_{k=1}^\infty(-1)^{k+1}\cdot\frac{x^{k}}{k}$$Damit ist die Potenzreihe klar.
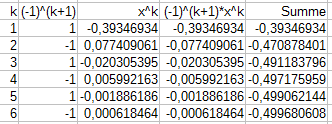
Nun sollen wir noch \(\ln\sqrt e=\frac{1}{2}\) näherungsweise bestimmen. Dafür müssten wir \(x=\sqrt e-1\approx1,718282\) setzen. Da dieses \(x>1\) ist, konvergiert die Taylor-Reihe nicht. Daher rechnen wir wie folgt:
$$\ln(1+x)=\ln\left(\left(\frac{1}{1+x}\right)^{-1}\right)=-\ln\left(\frac{1}{1+x}\right)=-\ln\left(\frac{1+x-x}{1+x}\right)$$$$\phantom{\ln(1+x)}=-\ln\left(1-\frac{x}{1+x}\right)$$Wir rechnen also:$$\ln(\sqrt e)=\ln(1+(\sqrt e-1))=-\ln\left(1-\frac{\sqrt e-1}{1+(\sqrt e-1)}\right)$$$$\phantom{\ln(\sqrt e)}=-\ln(\,1+(-0,39346934)\,)$$Mit \(x=-0,39346934\) erreichen wir die geforderte Genauigkeit bei \(k=5\):