Aufgabe:
(a) Es seien \( g, h: \Omega \rightarrow \mathbb{C} \) holomorph \( (\Omega \subset \mathbb{C} \) ein Bereich \( ), z_{0} \in \Omega \) eine einfache Nullstelle von \( h, g\left(z_{0}\right) \neq 0 \) und \( f=\frac{g}{h} . \) Zeigen Sie, dass
\( \operatorname{res}_{z 0} f=\frac{g\left(z_{0}\right)}{h^{\prime}\left(z_{0}\right)} \)
(b) Berechnen Sie für \( a>1 \) das Integral
\( \int \limits_{0}^{\infty} \frac{\mathrm{d} x}{1+x^{\alpha}} \)
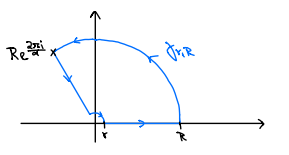
durch Anwenden des Residuensatzes auf die Funktion \( z \mapsto \frac{1}{1+z^{\alpha}} \) (welcher Definitionsbereich?) und den Weg \( \gamma_{r, R} \) aus dem Bild (plus Limiten \( R \rightarrow \infty, r \rightarrow 0 \) ).
Ich vermute, weil α reell ist, ergibt sich \( z^{\alpha}=r^{\alpha} e^{i \alpha \varphi} \) für \( z=r e^{i \varphi} \in \mathbb{C}_{\varphi 0} \) mit geeignetem \( \varphi_{0} \in \mathbb{R} \) und \( \varphi_{0}<\varphi<\varphi_{0}+2 \pi \)
Wisst ihr wie man ab da diese Integrale löst? Ich komme hier gar nicht weiter
Text erkannt:
\( \operatorname{Re}^{\frac{2 \pi i}{\alpha}}\{\prod \limits_{k}^{\gamma} \underbrace{\gamma x_{i} R} \)