FALLS
hätte gefragt werden wollen, dass die Parameter der Aufgabe so seien, dass ein Unternehmen zwei Produkte P1 und P2 produziert mit wöchentlich
- P1
-- Menge: Mittelwert 867, Standardabweichung 148
-- Preis: 12,50
- P2
-- Menge: Mittelwert 1086, Standardabweichung 245
-- Preis; 7,75
- Korrelationskoeffizient der Mengen P1 und P2: 0,68
DANN
ist meine Antwort:
Aus der in der Antwort zu https://www.mathelounge.de/798953 gegebenen Formel folgt, dass der angegebene Korrelationskoeffizient einer Kovarianz der Mengen von P1 und P2 von 24656,8 entspricht. Gefragt ist aber der Umsatz, also das Produkt aus stochastischer Menge mal konstantem Preis. Dabei gilt:
V(Umsatz P1) = E(Preis P1)2 * V(Menge P1) = 3 422 500
V(Umsatz P2) = E(Preis P2)2 * V(Menge P2) ≈ 3 605 252
Kovarianz ≈ 2 388 628
Aus der weiter oben in den Kommentaren zur Frage angegebenen Formel A.10 folgt eine Varianz des Gesamtwochenumsatzes von 11 805 007 was einer Standardabweichung von rund 3436 entspricht. Der Erwartungswert ist 867*12,50 + 1086*7,75 = 19254.
Die gesuchte Wahrscheinlichkeit ist somit
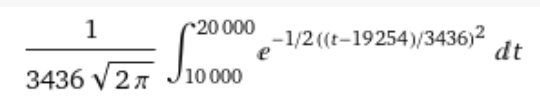
also rund 58 %.