Aloha :)
Für Gleichungen dieser gibt es leider keine allgemein gültige geschlossene Berechnungsformel. Manchmal hat man Glück und die Zahlenwerte lassen irgendwelche Tricks zu, aber diese sehe ich hier nicht. Wir müssen das Problem daher iterativ angehen:$$500\cdot t\cdot e^{-0,1t}\stackrel!=919,7\quad\Longleftrightarrow\quad t\cdot e^{-0,1t}\stackrel!=\frac{919,7}{500}\quad\Longleftrightarrow$$$$f(t)\!\coloneqq t\cdot e^{-0,1t}-1,8394\stackrel!=0$$Ein Plot verrät uns, dass es 2 Lösungen gibt, eine bei \(t\approx2\) und eine bei \(t\approx26\):
~plot~ x*e^(-x/10)-1,8394 ; [[0|30|0|2]] ~plot~
Zur Berechnung verwenden wir das Newton-Verfahren. Dabei starten wir mit einem Schätzwert \(t_0\), bestimmen die Gleichung der Tangente an die Kurve in diesem Punkt:$$g(t)=f(t_0)+f'(t_0)\cdot(t-t_0)$$und berechnen den Schnittpunkt \(t_1\) dieser Tangente mit der \(t\)-Achse:$$g(t_1)\stackrel!=0\implies f(t_0)+f'(t_0)\cdot(t_1-t_0)=0\implies f'(t_0)\cdot(t_1-t_0)=-f(t_0)\implies$$$$t_1=t_0-\frac{f(t_0)}{f'(t_0)}$$Dieser Schnittpunkt \(t_1\) ist dann unsere (bessere) Näherungslösung. Das Verfahren wird so lange wiederholt, bis die gewünschte Genauigkeit erreicht ist.
Für unsere Funktion \(f(t)\) von oben lautet die Iterationsformel:
$$t_1=t_0-\frac{t_0\cdot e^{-0,1t_0}-1,8394}{1\cdot e^{-0,1t_0}+t_0\cdot(-0,1)e^{-0,1t_0}}=t_0-\frac{t_0-1,8394e^{+0,1t_0}}{1-0,1\cdot t_0}$$
Das Newton-Verfahren konvergiert sehr schnell, nach nur 4 Schritten ändert sich das Ergebnis nicht mehr:
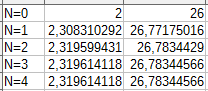
Wir haben also 2 Lösungen gefunden:$$t=2,319614118\quad\text{und}\quad t=26,78344566$$