Vektoren Prisma über dem Dreieck ABC Eckpunkte ermitteln

Question

Aufgabe:

Ein Prisma über dem Dreieck ABC hat eine Höhe von 5cm. Geben Sie die Koordinaten der drei weiteren Eckpunkte D, E und F an. Davor musste man die Koordinate C ermitteln. A(-2/-0,5/0) B(4/-0,5/0) liegen in der x1x2 Ebene. Die Höhe hc über AB beträgt 4cm.

Problem/Ansatz:

Für C habe ich (6/3,5/0) genommen. Ist es richtig? Wie komme ich auf die anderen Eckpunkte?

Answer 1

Hallo Tom,

Aufgaben dieser Art sind im Grunde total einfach wenn (ja wenn!) man sich ein Bild von der Situation macht. Unten siehst Du ein Bild von den drei Punkten, die die Grundfläche bilden. Und ...

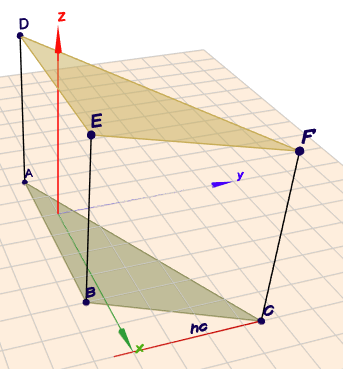
Und dann zieht man die Grundfläche einfach nach oben. D.h. da die Z-Koordinaten aller drei Punkte A, B und C gleich sind, muss man lediglich die Z-Koordinate um 5 erhöhen, um auf die Ecken D, E und F zu kommen.

Für C habe ich (6/3,5/0) genommen. Ist es richtig?

Das erfüllt die Bedingung \(h_c = 4\). Ich habe die Höhe \(h_c\) oben im Bild rot eingezeichnet.

Allerdings gibt es unendlich viele Dreiecke mit A und B und Höhe \(h_c\). War da vielleicht noch eine Bedingung gegeben? Sollte das Dreieck vielleicht gleichschenklig mit Basis \(AB\) sein?

Das sähe so aus:

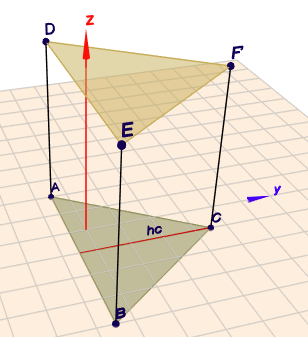
auch dieses Dreieck \(\triangle ABC\) hat die Höhe \(h_c=4\), aber \(C\) und \(F\) liegen in diesem Fall bei$$C = \begin{pmatrix}1\\ 3,5\\ 0\end{pmatrix}, \quad F= \begin{pmatrix}1\\ 3,5\\ 5\end{pmatrix}$$

(klick auf die Bilder, dann öffnet sich Geoknecht3D und Du kannst die Szene mit der Maus drehen und Du bekommst einen besseren Eindruck)

Gruß Werner

Comments

Ja es ist ein gleichschenkliges Dreieck. Lautet dann C (1/3,5/0) statt (6/3,5/0)?

E (4/-0,5/5) D(-2/-0,5/5) und F (1/3,5/5)?

Danke

---

Lautet dann C (1/3,5/0) statt (6/3,5/0)?

Ja! \(AB\) verläuft parallel zur X-Achse, da sowohl die Y- als auch die Z-Koordinate von \(A\) und \(B\) identisch ist. Da \(C\), die Spitze des gleichschenkligen Dreiecks, senkrecht über der Mitte von \(AB\) steht, muss die X-Koordinate von \(C\) der Mittelwert der X-Koordinaten von \(A\) und \(B\) sein. Formal:$$x_C = \frac 12(x_A + x_B) = \frac 12(-2 + 4) = 1$$die weiteren Koordinaten sind richtig. Mache Dir das an Hand der Bilder noch mal klar!

E (4/-0,5/5) D(-2/-0,5/5) und F (1/3,5/5)?

Wenn Du auf das zweite Bild geklickt hättest, würdest Du nicht mehr fragen! ;-)