Aufgabe: Bestimmen von Funktionstermen aus vorgegebenen Informationen!
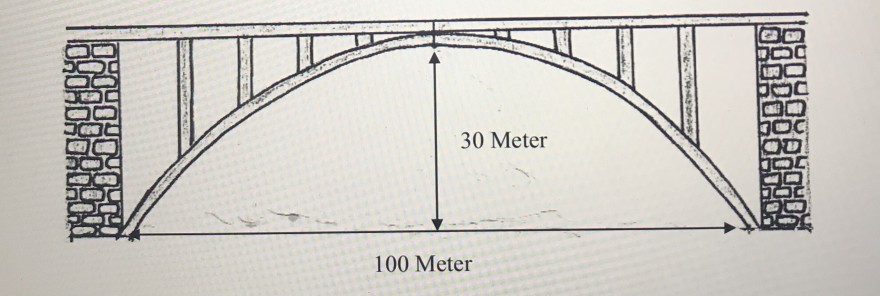
1.)Architectur: Bestimmen Sie die Form des Stützbogens!
Tipp: Überlegen Sie zuerst graphisch, welchen Funktion beschreibt ungefähr diesen Stützbogen. Danach Zeichen Sie zur Bestimmung der benötigten Punkte in Farbe ein geeignetes Koordinatensystem ein und ermitteln dann die Funktionsgleichung.
 2.) Schiffsfahrt:
2.) Schiffsfahrt:
Die Brücke in Aufgabe 1 ist eine Brücke über den Rhein kurz vor der Einmündung in die Nordsee. Wie breit darf ein Containerschiff sein, dass in den Hamburg Hafen möchte, dass auf der ganzen Breite seine Container 25 Meter hochgestapelt hat?