Hallo,
Legen Sie dazu ein geeignetes Koordinatensystem fest.
Das Koordinatensystem kannst Du natürlich legen wie Du willst. Ich habe das im folgenden so gelegt, dass die Ecke der Körper hinten, unten und links im Ursprung liegt, die Z-Achse nach oben und die Y-Achse nach rechts zeigt. Dann haben alle Punkte auf den Körper nicht-negative Koordinaten.
Ich bräuchte Hilfe bei: a) -> Gerade i und k
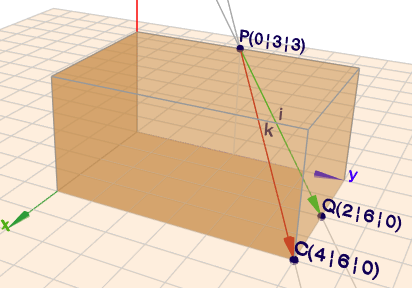
Der Quader hat die Abmessungen \(4 \times 6 \times 3\) in x-, y- und z-Richtung. Die unbezeichnete Ecke vorne rechts, durch die auch die Gerade \(k\) verläuft, bezeichne ich mit \(C\). Dann sind die Koordinaten von \(P\), \(C\) und \(Q\):$$P = \begin{pmatrix}0\\ 3\\ 3\end{pmatrix}, \quad C= \begin{pmatrix}4\\ 6\\ 0\end{pmatrix}, \quad Q=\begin{pmatrix}2\\ 6\\ 0\end{pmatrix}$$Und die Geradengleichungen für \(i\) (grün) und \(k\) (rot) sind$$i: \quad \vec x = P + \vec{PQ} \cdot r = \begin{pmatrix}0\\ 3\\ 3\end{pmatrix} + \begin{pmatrix}2\\ 3\\ -3\end{pmatrix}\cdot r \\ k: \quad \vec x = P + \vec{PC} \cdot s = \begin{pmatrix}0\\ 3\\ 3\end{pmatrix} + \begin{pmatrix}4\\ 3\\ -3\end{pmatrix} \cdot s$$
b) -> Gerade g
Die Gerade \(g\) ist identisch zur Geraden \(k\) aus Teil a) (s.o.) da \(P\) und \(C\) unverändert sind.
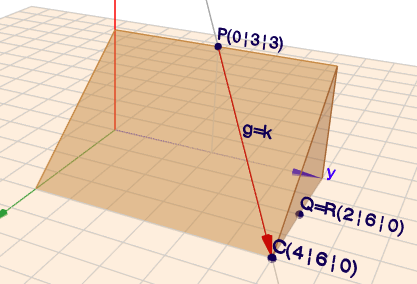
klick auf die Bilder, dann öffnet sich Geoknecht3D; und falls Du Fragen hast, so melde DIch bitte.
Gruß Werner