Hallo,
Die Angabe \(A=(x|\, -1|\, 3)\) ist im Prinzip eine Gerade \(h\), die durch einen Punkt$$A_{x=0} = \begin{pmatrix}0\\ -1\\ 3\end{pmatrix}$$verläuft und sich nur mit \(x\)-Koordinate ändert. Also$$h: \quad \vec x = \begin{pmatrix}0\\ -1\\ 3\end{pmatrix} + r\begin{pmatrix}1\\ 0\\ 0\end{pmatrix}$$Du berechnest also einen Schnittpunkt von \(h\) und \(g\)$$g: \quad \vec x = B + s(C-B) = \begin{pmatrix}-1\\ 4\\ 3\end{pmatrix} + s\begin{pmatrix}8\\ -8\\ 0\end{pmatrix}$$und den findet man bei \(r=4\) und \(s=5/8\). Also gibt es einen Schnittpunkt, wie auch folgendes Bild zeigt
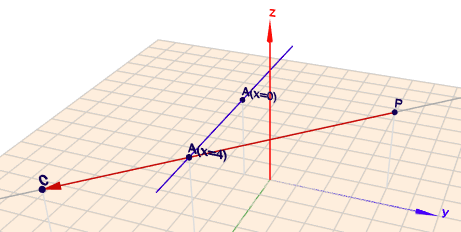
In diesem konkretem Fall kann man dies auch ohne Rechnung daran sehen, dass die Z-Koordinaten aller drei Punkte \(=3\), also identisch sind. Und da die Verbindungslinie zwischen \(B\) und \(C\) nicht parallel zur X-Achse verläuft, muss es auch einen Schnittpunkt geben!
Gruß Werner